Advertisements
Advertisements
प्रश्न
In a hexagon JKLMNO, side JK || ON and ∠K : ∠L : ∠M : ∠N = 6 : 5 : 4 : 3. Find the angle ∠K and ∠M.
उत्तर
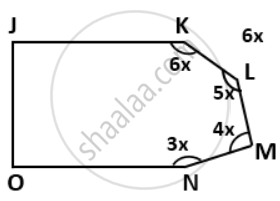
Given JK || ON
⇒ ∠J + ∠O = 180°
Also, ∠K : ∠L : ∠M : ∠N = 6 : 5 : 4 : 3
⇒ ∠K = 6x, ∠L = 5x, ∠M = 4x and ∠N = 3x
Since, ∠J + ∠K + ∠L + ∠M +∠N = 4 x 180°
⇒ (∠J + ∠O) +∠K + ∠L + ∠M + ∠N = 4 x 180°
⇒180° + 6x + 5x + 4x + 3x = 720°
⇒ 18x + 180° = 720°
⇒18x = 540°
⇒ x = 30°
Hence,
∠K = 6x
= 6 x 30°
= 180°
and
∠M = 4x
= 4 x 30°
= 120°.
APPEARS IN
संबंधित प्रश्न
The sum of the interior angles of a polygon is four times the sum of its exterior angles.
Find the number of sides in the polygon.
AB, BC, and CD are the three consecutive sides of a regular polygon. If BAC = 15°;
Find:
- Each interior angle of the polygon.
- Each exterior angle of the polygon.
- The number of sides of the polygon.
Two angles of an eight-sided polygon are 142o and 176o. If the remaining angles are equal to each other; find the magnitude of each of the equal angles.
In a pentagon ABCDE, AB is parallel to DC and ∠A: ∠E : ∠D = 3: 4: 5. Find angle E.
Find the sum of the interior angles of a polygon of: 9 sides
Find the number of sides in a regular polygon, when each interior angle is: 120°
Find the number of sides in a regular polygon, when each exterior angle is: 72°
The angles of a pentagon are 100°, 96°, 74°, 2x° and 3x°. Find the measures of the two angles 2x° and 3x°.
A heptagon has three angles equal to 120°, and the other four angles are equal. Find all the angles.
In a pentagon PQRST, ∠P = 100°, ∠Q = 120° and ∠S = ∠T. The sides PQ and SR, when produced meet at right angle. Find ∠QRS and ∠PTS.
