Question

In a ΔABC, AD is the bisector of ∠A, meeting side BC at D.

If BD = 2cm, AB = 5cm and DC = 3cm, find AC.

Answer 1

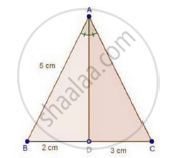
We have,

AD is the bisector of ∠A

We know that, the internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle.

`therefore"BD"/"DC"="AB"/"AC"`

`rArr2/3=5/"AC"`

`rArr"AC"=(5xx3)/2=15/2`

⇒ AC = 7.5 cm