Advertisements
Advertisements
Question
In the adjoining figure, point O is the centre of the cirlcle, seg OM ⊥ chord AB. If OM = 8cm, AB = 12 cm, then find OB.
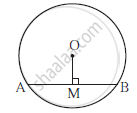
Solution
MB = 12 × AB = 12 × 12 = 6 cm (perpendicular drawn from the centre of the circle to the chord bisects the chord)
`OB^ = OM^2 + MB^2` .....................(Pythagoras thearem)
= `8^2 + 6^2`
= 64 + 36 = 100
∴ OB = 10 cm
shaalaa.com
Angle Subtended by the Arc to the Point on the Circle
Is there an error in this question or solution?
APPEARS IN
RELATED QUESTIONS
In the following figure, m(arc PMQ) = 130o, find ∠PQS.

In the following figure, secants containing chords RS and PQ of a circle intersects each other in point A in the exterior of a circle if m(arc PCR) = 26°, m(arc QDS) = 48°, then find:
(i) m∠PQR
(ii) m∠SPQ
(iii) m∠RAQ
If the length of an arc of the sector of a circle is 20 cm and if the radius is 7 cm, find the area of the sector.
