Advertisements
Advertisements
Question
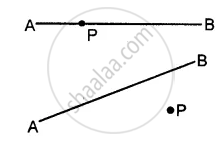
In each of the following, draw perpendicular through point P to the line segment AB :
(i)

(ii)

(iii)
Solution
(i) Steps of Construction :
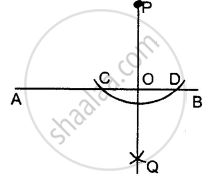
- With P as a centre, draw an arc of a suitable radius which cuts AB at points C and D.
- With C and D as centres, draw arcs of equal radii and let these arcs intersect each other at point Q.
[The radius of these arcs must be more than half of CD and both the arcs must be drawn on the other side] - Join P and Q
- Let PQ cut AB at the point O.
Thus, OP is the required perpendicular clearly, ∠AOP = ∠BOP = 90°
(ii) Steps of Construction :
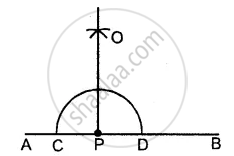
- With P as a centre, draw an arc of any suitable radius which cuts AB at points C and D.
- With C and D as centres, draw arcs of equal radii. Which intersect each other at point A.
[This radius must be more than half of CD and let these arc intersect each other at the point 0] - Join P and O. Then OP is the required perpendicular.
∠OPA = ∠OPB = 90°
(iii) Steps of Construction :
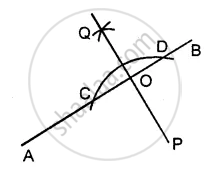
- With P as a centre, draw an arc of any suitable radius which cuts AB at points C and D.
- With C and D as a centre, draw arcs of equal radii
[The radius of these arcs must be more than half of CD and both the arcs must be drawn on the other side.]
and let these arcs intersect each other at the point Q. - Join Q and P. Let QP cut AB at the point O. Then OP is the required perpendicular.
Clearly, ∠AOP = ∠BOP = 90°
APPEARS IN
RELATED QUESTIONS
Draw a line segment AB = 5.5 cm. Mark a point P, such that PA = 6 cm and PB = 4.8 cm. From point P, draw a perpendicular to AB.
Draw a line segment of given length and construct a perpendicular bisector to line segment using scale and compass
8 cm
Draw a line segment of given length and construct a perpendicular bisector to line segment using scale and compass
7 cm
The line of symmetry of a line segment is the ______ bisector of the line segment.
Infinitely many perpendicular bisectors can be drawn to a given ray.
Draw the images of points A and B in line l of figure and name them as A’ and B’, respectively. Measure AB and A’B’. Are they equal?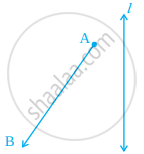
Draw a line segment of length 6 cm. Construct its perpendicular bisector. Measure the two parts of theline segment.
Draw a line segment of length 9.5 cm and construct its perpendicular bisector.
Draw the perpendicular bisector of `overline"XY"` whose length is 10.3 cm.
- Take any point P on the bisector drawn. Examine whether PX = PY
-
If M is the midpoint of `overline"XY"`, what can you say about the lengths MX and XY?
With `overline"PQ"` of length 6.1 cm as diameter, draw a circle.
