Advertisements
Advertisements
Question
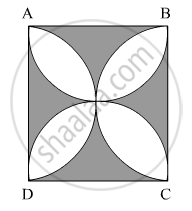
In Fig. 4, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region.
(use `pi=22/7`)
Solution

Let the four shaded regions be I, II, III and IV and the centres of the semicircles be P, Q, R and S, as shown in the figure.
It is given that the side of the square is 14 cm.
Now,
Area of region I + Area of region III = Area of the square − Areas of the semicircles with centres S and Q
=14×14−2×`1/2`×π×72 (∵ Radius of the semicircle=7 cm)
`=192-49xx22/7`
=196−154
=42 cm2
Similarly,
Area of region II + Area of region IV = Area of the square − Areas of the semicircles with centres P and R.
=14×14−2×`1/2`×π×72 (∵ Radius of the semicircle=7 cm)
=196−49×`22/7`
=196−154
=42 cm2
Thus,
Area of the shaded region = Area of region I + Area of region III + Area of region II + Area of region IV
= 42 cm2 + 42 cm2
= 84 cm2
APPEARS IN
RELATED QUESTIONS
The minute hand of a clock is 10cm long. Find the area of the face of the clock described by the minute hand between 9 A.M. and 9.35 A.M.
The circumference of two circles are in ratio 2:3. Find the ratio of their areas
What is the perimeter of a square which circumscribes a circle of radius a cm?
Find the radius of a circle whose perimeter and area are numerically equal.
A sector of 56°, cut out from a circle, contains 17.6 cm2. Find the radius of the circle.
Find the area and perimeter of the following sector :
Radius= 4.2 cm, angle at the centre is 60 °
Find the diameter of the sphere for the following :
Volume = `523 17/21` cm3
The diameter of a circular field is 56 m. Find its circumference and cost of fencing it at the rate of ₹80 per m. (Take π =`22/7`)
The inner circumference of a circular track is 264 m and the width of the track is 7 m. Find:
(i) the radius of the inner track.
(ii) the radius of the outer circumference.
(iii) the length of the outer circumference.
(iv) the cost of fencing the outer circumference at the rate of ₹50 per m.
