Advertisements
Advertisements
Question
In how many ways can this diagram be coloured subject to the following two conditions?
(i) Each of the smaller triangle is to be painted with one of three colours: red, blue or green.
(ii) No two adjacent regions have the same colour.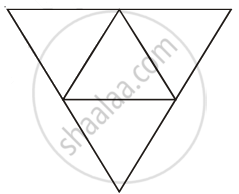
Solution
These conditions are satisfied exactly when we do as follows:
First paint the central triangle in any one of the three colours.
Next paint the remaining 3 triangles, with any one of the remaining two colours.
By the fundamental principle of counting
This can be done in 3 × 2 × 2 × 2 = 24 ways.
APPEARS IN
RELATED QUESTIONS
A coin is tossed 3 times and the outcomes are recorded. How many possible outcomes are there?
Given 5 flags of different colours, how many different signals can be generated if each signal requires the use of 2 flags, one below the other?
How many two letter words can be formed using letters from the word SPACE, when repetition of letters is allowed?
How many two letter words can be formed using letters from the word SPACE, when repetition of letters is allowed?
How many two letter words can be formed using letters from the word SPACE, when repetition of letters is not allowed?
How many three-digit numbers can be formed from the digits 0, 1, 3, 5, 6 if repetitions of digits are not allowed?
A letter lock contains 3 rings, each ring containing 5 different letters. Determine the maximum number of false trials that can be made before the lock is opened?
In a test, 5 questions are of the form 'state, true or false'. No student has got all answers correct. Also, the answer of every student is different. Find the number of students appeared for the test.
If numbers are formed using digits 2, 3, 4, 5, 6 without repetition, how many of them will exceed 400?
How many numbers formed with the digits 0, 1, 2, 5, 7, 8 will fall between 13 and 1000 if digits can be repeated?
Answer the following:
A hall has 12 lamps and every lamp can be switched on independently. Find the number of ways of illuminating the hall.
Three persons enter into a conference hall in which there are 10 seats. In how many ways they can take their seats?
Given four flags of different colours, how many different signals can be generated if each signal requires the use of three flags, one below the other?
Four children are running a race:
In how many ways can the first two places be filled?
How many numbers are there between 100 and 500 with the digits 0, 1, 2, 3, 4, 5? if repetition of digits allowed
Count the numbers between 999 and 10000 subject to the condition that there are at least one of the digits is repeated
To travel from a place A to place B, there are two different bus routes B1, B2, two different train routes T1, T2 and one air route A1. From place B to place C there is one bus route say B1, two different train routes say T1, T2 and one air route A1. Find the number of routes of commuting from place A to place C via place B without using similar mode of transportation
Count the total number of ways of answering 6 objective type questions, each question having 4 choices
Find the value of 3! – 2!
Find the value of `(12!)/(9! xx 3!)`
Evaluate `("n"!)/("r"!("n" - "r")!)` when for any n with r = 2
Choose the correct alternative:
The number of 5 digit numbers all digits of which are odd i
How many numbers are there between 99 and 1000 having 7 in the units place?
How many numbers are there between 99 and 1000 having atleast one of their digits 7?
Find the number of integers greater than 7000 that can be formed with the digits 3, 5, 7, 8 and 9 where no digits are repeated.
The number of possible outcomes when a coin is tossed 6 times is ______.
The sum of the digits in unit place of all the numbers formed with the help of 3, 4, 5 and 6 taken all at a time is ______.
The number of six-digit numbers, all digits of which are odd is ______.
There will be only 24 selections containing at least one red ball out of a bag containing 4 red and 5 black balls. It is being given that the balls of the same colour are identical.
