Advertisements
Advertisements
Question
In previous questions 3 and 4, what is the net power absorbed by each circuit over a complete cycle. Explain your answer.
Solution
In the inductive circuit,
rms value of current, I = 15.92 A
rms value of voltage, V = 220 V
Hence, the net power absorbed can be obtained by the relation,
P = VI cos `phi`
Where,
`phi` = Phase difference between V and I
For a pure inductive circuit, the phase difference between alternating voltage and current is 90°, i.e., `phi` = 90°.
Hence, P = 0, i.e., the net power is zero.
In the capacitive circuit,
rms value of current, I = 2.49 A
rms value of voltage, V = 110 V
Hence, the net power absorbed can be obtained as:
P = VI Cos `phi`
For a pure capacitive circuit, the phase difference between alternating voltage and current is 90°, i.e., `phi` = 90°.
Hence, P = 0, i.e., the net power is zero.
APPEARS IN
RELATED QUESTIONS
An a.c. source of voltage V = V0 sin ωt is connected to a series combination of L, C, and R. Use the phasor diagram to obtain the expression for an impedance of a circuit and the phase angle between voltage and current. Find the condition when current will be in phase with the voltage. What is the circuit in this condition called?
When an AC source is connected to an ideal inductor show that the average power supplied by the source over a complete cycle is zero.
In a series LR circuit, XL = R and power factor of the circuit is P1. When capacitor with capacitance C such that XL = XC is put in series, the power factor becomes P2. Calculate P1/P2
The power factor of an a.c. circuit is 0.5. What is the phase difference between voltage and current in this circuit ?
A series AC circuit has a resistance of 4 Ω and a reactance of 3 Ω. The impedance of the circuit is
In an AC series circuit, the instantaneous currt is zero when the instantaneous voltage is maximum. Connected to the source may be a
(a) pure inductor
(b) pure capacitor
(c) pure resistor
(d) combination of an inductor and a capacitor
The current in a discharging LR circuit is given by i = i0 e−t/τ , where τ is the time constant of the circuit. Calculate the rms current for the period t = 0 to t = τ.
A coil has a resistance of 10 Ω and an inductance of 0.4 henry. It is connected to an AC source of 6.5 V, `30/pi Hz`. Find the average power consumed in the circuit.
Consider the situation of the previous problem. Find the average electric field energy stored in the capacitor and the average magnetic field energy stored in the coil.
What is the value of power factor for a pure resistor connected to an alternating current source ?
An ac circuit as shown in the figure has an inductor of inductance L and a resistor of resistance R connected in series. Using the phasor diagram, explain why the voltage in the circuit will lead the current in phase.
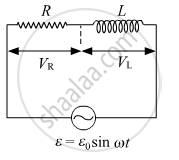
Suppose the circuit has a resistance of 15 Ω. Obtain the average power transferred to each element of the circuit, and the total power absorbed.
Which of the following quantities remains constant in a step-down Transformer?
The power factor of an a.c circuit having resistance R and inductance L Connected in series to an a.c source of angular frequency co is.
A 100 Ω electric iron is connected to 200 V, 50 Hz ac source. Calculate average power delivered to iron, peak power and energy spent in one minute?
In the series LCR circuit, the power dissipation is through ______
