Advertisements
Advertisements
Question
In a series RC circuit with an AC source, R = 300 Ω, C = 25 μF, ε0 = 50 V and ν = 50/π Hz. Find the peak current and the average power dissipated in the circuit.
Solution
Given:
Resistance of the series RC circuit, R = 300 Ω
Capacitance of the series RC circuit, C = 25 μF
Peak value of voltage, ε0 = 50 V
Frequency of the AC source, ν = 50/ `pi` Hz
Capacitive reactance (Xc) is given by,
`X_C = 1/(omegaC)`
Here, ω = angular frequency of AC source
C = capacitive reactance of capacitance
∴ `X_C = 1/(2xx50/pixx25xx10^-6)`
⇒ `X_C = 10^4/25 Ω`
Net reactance of the series RC circuit`(Z) = sqrt(R^2 + (X_C)^2`
⇒ Z =`sqrt((300)^2 + (10^4/25)^2`
= `sqrt((300)^2 + (400)^2 = 500 Ω`
(a) Peak value of current `(I_0)` is given by,
`I_0 = (epsilon_0)/z`
⇒ `I_0 = 50/500 = 0.1 A`
(b) Average power dissipated in the circuit (P) is given by,
`P = epsilon_{rms}l_{rms} cosØ`
`epsilon_{rms] = epsilon_0/sqrt2`
`∴ P = E_0/sqrt2xx I_0/sqrt2xxR/Z`
⇒ P =`(50xx0.1xx300)/(2xx500)`
⇒ `P = 3/2 = 1.5 W`
APPEARS IN
RELATED QUESTIONS
A device X is connected across an ac source of voltage V = V0 sin ωt. The current through X is given as
`I = I_0 sin (omega t + pi/2 )`
1) Identify the device X and write the expression for its reactance.
2) Draw graphs showing the variation of voltage and current with time over one cycle of ac, for X.
3) How does the reactance of the device X vary with the frequency of the ac? Show this variation graphically.
4) Draw the phasor diagram for the device X.
The voltage and current in a series AC circuit are given by V = V0cos ωt and i = i0 sin ωt. What is the power dissipated in the circuit?
Can the peak voltage across the inductor be greater than the peak voltage of the source in an LCR circuit?
Can a hot-wire ammeter be used to measure a direct current of constant value? Do we have to change the graduations?
An alternating current is given by i = i1 cos ωt + i2 sin ωt. The rms current is given by
A constant current of 2.8 A exists in a resistor. The rms current is
Find the time required for a 50 Hz alternating current to change its value from zero to the rms value.
An electric bulb is designed to operate at 12 volts DC. If this bulb is connected to an AC source and gives normal brightness, what would be the peak voltage of the source?
The peak power consumed by a resistive coil, when connected to an AC source, is 80 W. Find the energy consumed by the coil in 100 seconds, which is many times larger than the time period of the source.
A capacitor of capacitance 10 μF is connected to an oscillator with output voltage ε = (10 V) sin ωt. Find the peak currents in the circuit for ω = 10 s−1, 100 s−1, 500 s−1 and 1000 s−1.
A coil of inductance 5.0 mH and negligible resistance is connected to the oscillator of the previous problem. Find the peak currents in the circuit for ω = 100 s−1, 500 s−1, 1000 s−1.
A resistor of resistance 100 Ω is connected to an AC source ε = (12 V) sin (250 π s−1)t. Find the energy dissipated as heat during t = 0 to t = 1.0 ms.
Answer the following question.
A small town with a demand of 1200 kW of electric power at 220 V is situated 20 km away from an electric plant generating power at 440 V. The resistance of the two wirelines carrying power is 0.5 Ω per km. The town gets the power from the line through a 4000-220 V step-down transformer at a sub-station in the town. Estimate the line power loss in the form of heat.
The peak voltage of an ac supply is 300 V. What is the rms voltage?
The period of oscillation of a simple pendulum is T = `2π sqrt"L"/"g"`. The measured value of L is 20.0 cm known to have 1 mm accuracy and the time for 100 oscillations of the pendulum is found to be 90 s using a wristwatch of ls resolution. The accuracy in the determination of g is:
RMS value of an alternating current flowing in a circuit is 5A. Calculate its peak value.
In the Figure below, the current-voltage graphs for a conductor are given at two different temperatures, T1 and T2.
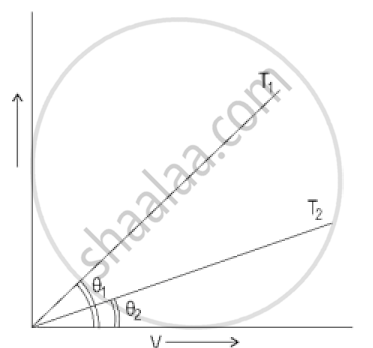
- At which temperature T1 or T2 is the resistance higher?
- Which temperature (T1 or T2) is higher?
