Advertisements
Advertisements
प्रश्न
In a series RC circuit with an AC source, R = 300 Ω, C = 25 μF, ε0 = 50 V and ν = 50/π Hz. Find the peak current and the average power dissipated in the circuit.
उत्तर
Given:
Resistance of the series RC circuit, R = 300 Ω
Capacitance of the series RC circuit, C = 25 μF
Peak value of voltage, ε0 = 50 V
Frequency of the AC source, ν = 50/ `pi` Hz
Capacitive reactance (Xc) is given by,
`X_C = 1/(omegaC)`
Here, ω = angular frequency of AC source
C = capacitive reactance of capacitance
∴ `X_C = 1/(2xx50/pixx25xx10^-6)`
⇒ `X_C = 10^4/25 Ω`
Net reactance of the series RC circuit`(Z) = sqrt(R^2 + (X_C)^2`
⇒ Z =`sqrt((300)^2 + (10^4/25)^2`
= `sqrt((300)^2 + (400)^2 = 500 Ω`
(a) Peak value of current `(I_0)` is given by,
`I_0 = (epsilon_0)/z`
⇒ `I_0 = 50/500 = 0.1 A`
(b) Average power dissipated in the circuit (P) is given by,
`P = epsilon_{rms}l_{rms} cosØ`
`epsilon_{rms] = epsilon_0/sqrt2`
`∴ P = E_0/sqrt2xx I_0/sqrt2xxR/Z`
⇒ P =`(50xx0.1xx300)/(2xx500)`
⇒ `P = 3/2 = 1.5 W`
APPEARS IN
संबंधित प्रश्न
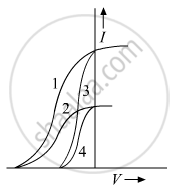
The given graph shows the variation of photo-electric current (I) versus applied voltage (V) for two difference photosensitive materials and for two different intensities of the incident radiations. Identify the pairs of curves that correspond to different materials but same intensity of incident radiation.
Two alternating currents are given by `i_1 = i_0 sin wt and i_2 = i_0 sin (wt + pi/3)` Will the rms values of the currents be equal or different?
Can the peak voltage across the inductor be greater than the peak voltage of the source in an LCR circuit?
Can a hot-wire ammeter be used to measure a direct current of constant value? Do we have to change the graduations?
A constant current of 2.8 A exists in a resistor. The rms current is
An electric bulb is designed to operate at 12 volts DC. If this bulb is connected to an AC source and gives normal brightness, what would be the peak voltage of the source?
The peak power consumed by a resistive coil, when connected to an AC source, is 80 W. Find the energy consumed by the coil in 100 seconds, which is many times larger than the time period of the source.
The dielectric strength of air is 3.0 × 106 V/m. A parallel-plate air-capacitor has area 20 cm2 and plate separation 0.10 mm. Find the maximum rms voltage of an AC source that can be safely connected to this capacitor.
A coil of inductance 5.0 mH and negligible resistance is connected to the oscillator of the previous problem. Find the peak currents in the circuit for ω = 100 s−1, 500 s−1, 1000 s−1.
The rms value of current in an ac circuit is 10 A. What is the peak current?
A small town with a demand of 800 kW of electric power at 220 V is situated 15 km away from an electric plant generating power at 440 V. The resistance of the two wire line carrying power is 0.5 Ω per km. The town gets power from the line through a 4000-220 V step-down transformer at a sub-station in the town.
(a) Estimate the line power loss in the form of heat.
(b) How much power must the plant supply, assuming there is negligible power loss due to leakage?
(c) Characterise the step up transformer at the plant.
Do the same with the replacement of the earlier transformer by a 40,000-220 V step-down transformer (Neglect, as before, leakage losses though this may not be a good assumption any longer because of the very high voltage transmission involved). Hence, explain why high voltage transmission is preferred?
If `|vec"A" xx vec"B"| = sqrt3 vec"A" . vec"B"` then the value of is `|vec"A" xx vec"B"|` is
Phase diffn between voltage and current in a capacitor in A.C Circuit is.
RMS value of an alternating current flowing in a circuit is 5A. Calculate its peak value.
