Advertisements
Advertisements
Question
In the figure, given below, O is the centre of the circumcircle of triangle XYZ.
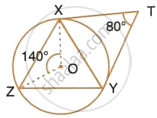
Tangents at X and Y intersect at point T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
Solution
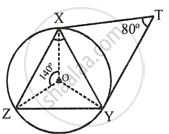
In the figure, a circle with centre O, is the circumcircle of triangle XYZ.
∠XOZ = 140° ...(Given)
Tangents at X and Y intersect at point T, such that ∠XTY = 80°
∴ ∠XOY = 180° – 80° = 100°
But, ∠XOY + ∠YOZ + ∠ZOX = 360° ...[Angles at a point]
`=>` 100° + ∠YOZ + 140° = 360°
`=>` 240° + ∠YOZ = 360°
`=>` ∠YOZ = 360° – 240°
`=>` ∠YOZ = 120°
Now arc YZ subtends ∠YOZ at the centre and ∠YXZ at the remaining part of the circle.
∴ ∠YOZ = 2∠YXZ
`=> ∠YXZ = 1/2 ∠YOZ`
`=> ∠YXZ = 1/2 xx 120^circ = 60^circ`
APPEARS IN
RELATED QUESTIONS
P is the mid-point of an arc APB of a circle. Prove that the tangent drawn at P will be parallel to the chord AB.
In the given figure, MN is the common chord of two intersecting circles and AB is their common tangent.
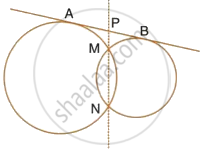
Prove that the line NM produced bisects AB at P.
Chords AB and CD of a circle when extended meet at point X. Given AB = 4 cm, BX = 6 cm and XD = 5 cm, calculate the length of CD.
