Advertisements
Advertisements
Question
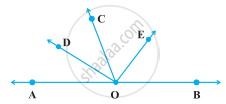
In the following figure, OD is the bisector of ∠AOC, OE is the bisector of ∠BOC and OD ⊥ OE. Show that the points A, O and B are collinear.
Solution
Given In the following figure, OD ⊥ OE, OD and OE are the bisectors of ∠AOC and ∠BOC.
To show Points A, O and B are collinear i.e., AOB is a straight line.
Proof Since, OD and OE bisect angles ∠AOC and ∠BOC, respectively.
∠AOC = 2∠DOC ...(i)
And ∠COB = 2∠COE ...(ii)
On adding equations (i) and (ii), we get
∠AOC + ∠COB = 2∠DOC + 2∠COE
⇒ ∠AOC + ∠COB = 2(∠DOC + ∠COE)
⇒ ∠AOC + ∠COB = 2∠DOE
⇒ ∠AOC + ∠COB = 2 × 90° ...[∴ OD ⊥ OE]
⇒ ∠AOC + ∠COB = 180°
∴ ∠AOB = 180°
So, ∠AOC and ∠COB are forming linear pair.
Also, AOB is a straight line.
Hence, points A, O and B are collinear.
APPEARS IN
RELATED QUESTIONS
In the following figure, if AB || CD || EF, PQ || RS, ∠RQD = 25° and ∠CQP = 60°, then ∠QRS is equal to ______.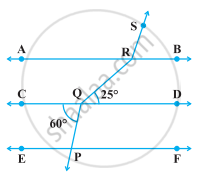
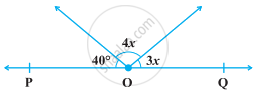
In the following figure, POQ is a line. The value of x is ______.
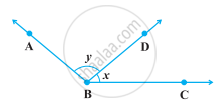
For what value of x + y in figure will ABC be a line? Justify your answer.
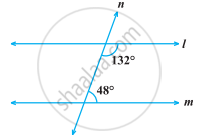
In the following figure, which of the two lines are parallel and why?
 |
 |
In the following figure, ∠1 = 60° and ∠6 = 120°. Show that the lines m and n are parallel.