Advertisements
Advertisements
Question
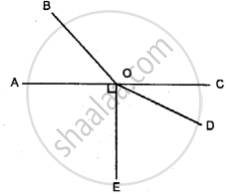
In the given figure ; AOC-is a straight line. If angle AOB = 50°, angle AOE = 90° and angle COD = 25° ; find the measure of:
(i) angle BOC
(ii) angle EOD
(iii) obtuse angle BOD
(iv) reflex angle BOD
(v) reflex angle COE.
Solution
(i) ∠AOB + ∠BOC = 180° (Linear pairs of angle)
⇒ 50° +∠BOC = 180°
⇒ ∠BOC = 180° – 50° = 130°
⇒ ∠BOC = 130°
(ii) ∠EOD + ∠COD = 90° (∵AOE = 90°)
⇒ ∠EOD + 25° = 90°
⇒ ∠EOD + 25° = 90°
⇒ ∠EOD = 90° – 25°
⇒ ∠EOD = 65°
(iii) ∠BOD = ∠BOC + COD
= 130° + 25° = 155°
(iv) Reflex ∠BOD = 360° – ∠BOD
= 360°- 155° = 205°
(v) Reflex ∠COE = 360° – ∠COE
= 360° (∠COD + ∠EOD)
= 360° – (25° + 65°)
= 360° – 90° = 270°
APPEARS IN
RELATED QUESTIONS
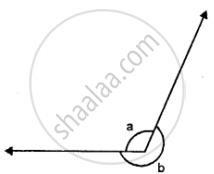
In the given figure if: b = 200 ; find a.
Write the complement angle of: (x – 10)°
Write the supplement angle of: 49°
Write the supplement angle of: (x – 30)°
Write the complement angle of: `2/5` of 70°
`1/3` of 150°
Find the angle that is equal to its complement?
Find the angle that is equal to its supplement?
The measures of two complementary angles are (2x – 7)° and (x + 4)°. Find x.
Find the angle formed by the arms of a clock at 9 O’clock.
