Advertisements
Advertisements
प्रश्न
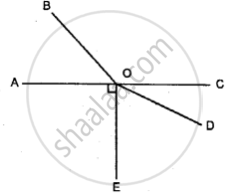
In the given figure ; AOC-is a straight line. If angle AOB = 50°, angle AOE = 90° and angle COD = 25° ; find the measure of:
(i) angle BOC
(ii) angle EOD
(iii) obtuse angle BOD
(iv) reflex angle BOD
(v) reflex angle COE.
उत्तर
(i) ∠AOB + ∠BOC = 180° (Linear pairs of angle)
⇒ 50° +∠BOC = 180°
⇒ ∠BOC = 180° – 50° = 130°
⇒ ∠BOC = 130°
(ii) ∠EOD + ∠COD = 90° (∵AOE = 90°)
⇒ ∠EOD + 25° = 90°
⇒ ∠EOD + 25° = 90°
⇒ ∠EOD = 90° – 25°
⇒ ∠EOD = 65°
(iii) ∠BOD = ∠BOC + COD
= 130° + 25° = 155°
(iv) Reflex ∠BOD = 360° – ∠BOD
= 360°- 155° = 205°
(v) Reflex ∠COE = 360° – ∠COE
= 360° (∠COD + ∠EOD)
= 360° – (25° + 65°)
= 360° – 90° = 270°
APPEARS IN
संबंधित प्रश्न
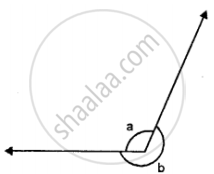
In the given figure if: b = 200 ; find a.
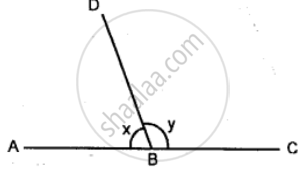
In the given diagram, ABC is a straight line. If x = 53°, find y.
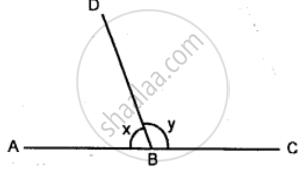
In the given diagram, ABC is a straight line. If y =`1 1/2` right angles; find x.
In the given figure:
(i) If ∠AOB = 45°, ∠BOC = 30° and ∠AOD= 110°; find : angles COD and BOD.
(ii) If ∠BOC = ∠DOC = 34° and ∠AOD = 120° ; find : angle AOB and angle AOC.
(iii) If ∠AOB = ∠BOC = ∠COD = 38° find : reflex angle AOC and reflex angle AOD.
Write the complement angle of: (x – 10)°
Write the complement angle of: 20° + y°
Write the complement angle of: `1/6` of 90°
Two supplementary angles are in the ratio 7 : 11. Find the angles.
Explain what do you understand by Adjacent angles?
Two adjacent angles forming a linear pair are in the ratio 7:5, find the angles.
