Advertisements
Advertisements
प्रश्न
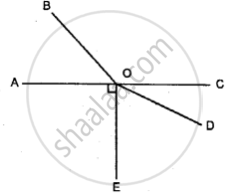
In the given figure ; AOC-is a straight line. If angle AOB = 50°, angle AOE = 90° and angle COD = 25° ; find the measure of:
(i) angle BOC
(ii) angle EOD
(iii) obtuse angle BOD
(iv) reflex angle BOD
(v) reflex angle COE.
उत्तर
(i) ∠AOB + ∠BOC = 180° (Linear pairs of angle)
⇒ 50° +∠BOC = 180°
⇒ ∠BOC = 180° – 50° = 130°
⇒ ∠BOC = 130°
(ii) ∠EOD + ∠COD = 90° (∵AOE = 90°)
⇒ ∠EOD + 25° = 90°
⇒ ∠EOD + 25° = 90°
⇒ ∠EOD = 90° – 25°
⇒ ∠EOD = 65°
(iii) ∠BOD = ∠BOC + COD
= 130° + 25° = 155°
(iv) Reflex ∠BOD = 360° – ∠BOD
= 360°- 155° = 205°
(v) Reflex ∠COE = 360° – ∠COE
= 360° (∠COD + ∠EOD)
= 360° – (25° + 65°)
= 360° – 90° = 270°
APPEARS IN
संबंधित प्रश्न
In the given figure if: a = 130° ; find b.
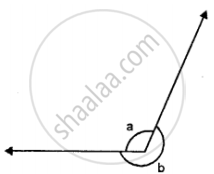
In the given figure if: a = 5/3 right angle, find b

In the given diagram, ABC is a straight line. If x = 53°, find y.
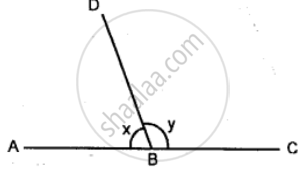
In the given diagram, ABC is a straight line. If y =`1 1/2` right angles; find x.
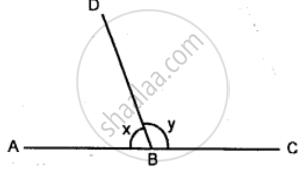
In the given figure, lines AB and CD intersect at point O.
(i) Find the value of ∠a.
(ii) Name all the pairs of vertically opposite angles.
(iii) Name all the pairs of adjacent angles.
(iv) Name all the reflex angles formed and write the measure of each.
Write the complement angle of: 45°
Write the complement angle of: 20° + y°
Write the complement angle of: `1/5` of 160°
50% of 120°
Find the angle formed by the arms of a clock at 3 O’clock.
