Advertisements
Chapters
2: Estimation
3: Numbers in India and International System (With Comparison)
4: Place Value
5: Natural Numbers and Whole Numbers (Including Patterns)
6: Negative Numbers and Integers
7: Number Line
8: HCF and LCM
9: Playing with Numbers
10: Sets
11: Ratio
12: Proportion (Including Word Problems)
13: Unitary Method
14: Fractions
15: Decimal Fractions
16: Percent (Percentage)
17: Idea of Speed, Distance and Time
18: Fundamental Concepts of algebra
19: Fundamental Operations (Related to Algebraic Expressions)
20: Substitution (Including Use of Brackets as Grouping Symbols)
21: Framing Algebraic Expressions (Including Evaluation)
22: Simple (Linear) Equations (Including Word Problems)
23: Fundamental Concepts geometry
▶ 24: Angles (With their Types)
25: Properties of Angles and Lines (Including Parallel Lines)
26: Triangles (Including Types, Properties and Constructions)
27: Quadrilateral
28: Polygons
29: The Circle
30: Revision Exercise Symmetry (Including Constructions on Symmetry)
31: Recognition of Solids
32: Perimeter and Area of Plane Figures
33: Data Handling (Including Pictograph and Bar Graph)
34: Mean and Median
![Selina solutions for Mathematics [English] Class 6 chapter 24 - Angles (With their Types) - Shaalaa.com](/images/mathematics-english-class-6_6:44f3c4f6e33345f4bf41a86d406bf37f.jpg "Selina solutions for Mathematics [English] Class 6 chapter 24 - Angles (With their Types)")
Advertisements
Solutions for Chapter 24: Angles (With their Types)
Below listed, you can find solutions for Chapter 24 of CISCE Selina for Mathematics [English] Class 6.
Selina solutions for Mathematics [English] Class 6 24 Angles (With their Types) Exercise 24 (A)
State if the angle given below, write the name of the vertex, the name of the arm and the name of the angle.
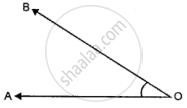
State if the angle given below, write the name of the vertex, the name of the arm and the name of the angle.
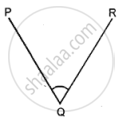
State if the angle given below, write the name of the vertex, the name of the arm and the name of the angle.
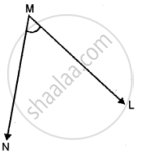
Name the angles marked by letters a, b, c, x and y.
Name the points in the interior of the angle PQR.
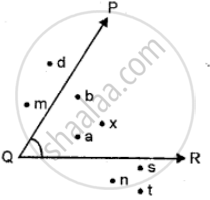
Name the points in the exterior of the angle PQR.
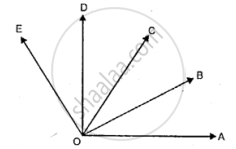
In the given figure, figure out the number of angles formed within the arms OA and OE.
Add: 29° 16′ 23″ and 8° 27′ 12″
Add: 9° 45’56” and 73° 8′ 15″
Add: 56° 38′ and 27° 42’30”
Add: 47° and 61° 17’4″
In the figure, given below name the three pairs of adjacent angles.
In the figure, given below name the two acute angles.
In the figure, given below name the two obtuse angles
In the figure, given below name the two reflex angles.
In the given figure; PQR is a straight line. If: ∠SQR = 75°; find ∠PQS.
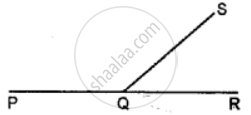
In the given figure; PQR is a straight line. If: ∠PQS = 110°; find ∠RQS.
In the given figure ; AOC-is a straight line. If angle AOB = 50°, angle AOE = 90° and angle COD = 25° ; find the measure of:
(i) angle BOC
(ii) angle EOD
(iii) obtuse angle BOD
(iv) reflex angle BOD
(v) reflex angle COE.
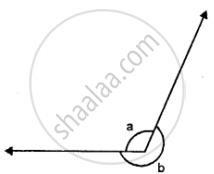
In the given figure if: a = 130° ; find b.
In the given figure if: b = 200 ; find a.
In the given figure if: a = 5/3 right angle, find b
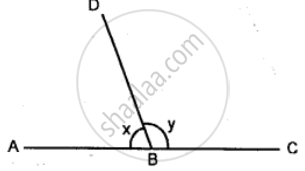
In the given diagram, ABC is a straight line. If x = 53°, find y.
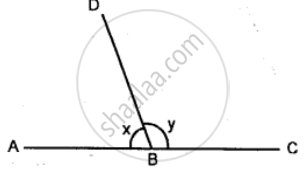
In the given diagram, ABC is a straight line. If y =`1 1/2` right angles; find x.
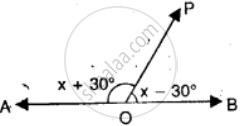
In the given figure, AOB is a straight line. Find the value of x and also answer each of the following:
(i) ∠AOP = ……..
(ii) ∠BOP = ……..
(iii) which angle is obtuse?
(iv) which angle is acute?
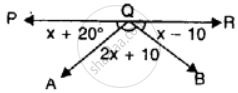
In the given figure, PQR is a straight line. Find x. Then complete the following:
(i) ∠AQB = _______
(ii) ∠BQP = _______
(iii) ∠AQR = _______
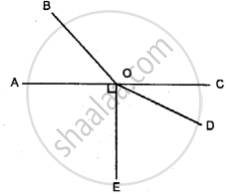
In the given figure, lines AB and CD intersect at point O.
(i) Find the value of ∠a.
(ii) Name all the pairs of vertically opposite angles.
(iii) Name all the pairs of adjacent angles.
(iv) Name all the reflex angles formed and write the measure of each.
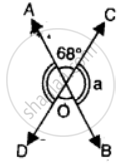
In the given figure:
(i) If ∠AOB = 45°, ∠BOC = 30° and ∠AOD= 110°; find : angles COD and BOD.
(ii) If ∠BOC = ∠DOC = 34° and ∠AOD = 120° ; find : angle AOB and angle AOC.
(iii) If ∠AOB = ∠BOC = ∠COD = 38° find : reflex angle AOC and reflex angle AOD.
Selina solutions for Mathematics [English] Class 6 24 Angles (With their Types) Exercise 24 (B)
Write the complement angle of: 45°
Write the complement of an angle of measure x°.
Write the complement angle of: (x – 10)°
Write the complement angle of: 20° + y°
Write the supplement angle of: 49°
Write the supplement angle of: 111°
Write the supplement angle of: (x – 30)°
Write the supplement angle of: 20° + y°
Write the complement angle of: `1/2` of 60°
Write the complement angle of: `1/5` of 160°
Write the complement angle of: `2/5` of 70°
Write the complement angle of: `1/6` of 90°
50% of 120°
`1/3` of 150°
60% of 100°
`3/4` of 160°
Find the angle that is equal to its complement?
Find the angle that is equal to its supplement?
Two complementary angles are in the ratio 7 : 8. Find the angles.
Two supplementary angles are in the ratio 7 : 11. Find the angles.
The measures of two complementary angles are (2x – 7)° and (x + 4)°. Find x.
The measures of two supplementary angles are (3x + 15)° and (2x + 5)°. Find x.
For an angle x°, find:
(i) the complementary angle
(ii) the supplementary angle
(iii) the value of x° if its supplementary angle is three times its complementary angle.
Selina solutions for Mathematics [English] Class 6 24 Angles (With their Types) Revision Exercise
Explain what do you understand by Adjacent angles?
Explain what do you understand by complementary angles?
Explain what do you understand by supplementary angles?
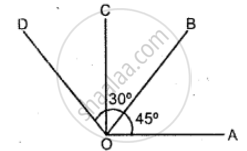
Find the value of ‘x’ for the following figure:
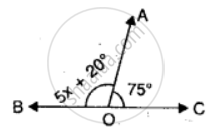
Find the value of ‘x’ for the following figure:
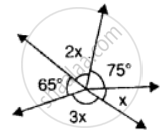
Find the value of ‘x’ for the following figure:
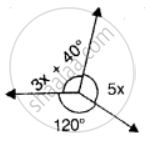
Find the number of degrees in an angle that is `3/5` of a right angle.
Find the number of degrees in an angle that is 0.2 times of a straight line angle.
In the given figure; AB, CD and EF are straight lines. Name the pair of angles forming the straight line angles.
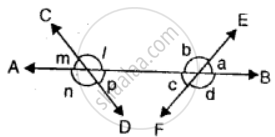
In the given figure; AB, CD and EF are straight lines. Name the pair of angles forming the vertically opposite angles.
Find the complement of: `2/5 "of" 210^circ`
Find the complement of 0.4 times of 130°.
Find the supplement of: `5/7` of 154°
Find the supplement of 0.7 times of 150°
Two complementary angles are in the ratio 7 : 8. Find the angles.
Two supplementary angles are in the ratio 7 : 5. Find the angles.
Two supplementary angles are (5x – 82°) and (4x + 73°). Find the value of x.
Find the angle formed by the arms of a clock at 3 O’clock.
Find the angle formed by the arms of a clock at 6 O’clock.
Find the angle formed by the arms of a clock at 9 O’clock.
Find the angle formed by the arms of a clock at 12 O’clock.
For an angle y°, find:
(i) its supplementary angle.
(ii) its complementary angle.
(iii) the value of y° if its supplement is four times its complement.
Use the adjoining figure to find: (i) ∠BOD (ii) ∠AOC
Two adjacent angles forming a linear pair are in the ratio 7:5, find the angles.
Find the angle that is three times its complementary angle.
An angle is one-thirds of a straight line angle; find:
(i) the angle
(ii) the complement and the supplement of the angle obtained above.
Solutions for 24: Angles (With their Types)
Selina solutions for Mathematics [English] Class 6 chapter 24 - Angles (With their Types)
Shaalaa.com has the CISCE Mathematics Mathematics [English] Class 6 CISCE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Selina solutions for Mathematics Mathematics [English] Class 6 CISCE 24 (Angles (With their Types)) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Selina textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 6 chapter 24 Angles (With their Types) are Measure of Angles, Types of Angles, Introduction to Lines and Angles.
Using Selina Mathematics [English] Class 6 solutions Angles (With their Types) exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Selina Solutions are essential questions that can be asked in the final exam. Maximum CISCE Mathematics [English] Class 6 students prefer Selina Textbook Solutions to score more in exams.
Get the free view of Chapter 24, Angles (With their Types) Mathematics [English] Class 6 additional questions for Mathematics Mathematics [English] Class 6 CISCE, and you can use Shaalaa.com to keep it handy for your exam preparation.
