Advertisements
Advertisements
प्रश्न
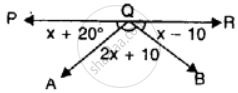
In the given figure, PQR is a straight line. Find x. Then complete the following:
(i) ∠AQB = _______
(ii) ∠BQP = _______
(iii) ∠AQR = _______
उत्तर
PQR is a straight line
∠AQP=x + 20°
∠AQB = 2x + 10°
∠BQR = x – 10°
But ∠AQP + ∠AQB + ∠BQR = 180°
⇒ x + 20° + 2x + 10° + x - 10°= 180°
⇒ 4x + 20°= 180°
⇒ 4x = 180° - 20°= 160°
⇒ x = `160^circ/4 = 40^circ`
(i) ∠AQB = 2x + 10° = 2 x 40° + 10° = 80° + 10° = 90°
∠AQP = x + 2(T = 40° + 20° = 60°
∠BQR = x – 10° = 40° – 10° = 30°
(ii) ∠BQP = ∠AQP + ∠AQB = 60° + 90° = 150°
(iii) ∠AQR = ∠AQB + ∠BQR = 90° + 30° = 120°
APPEARS IN
संबंधित प्रश्न
In the given figure ; AOC-is a straight line. If angle AOB = 50°, angle AOE = 90° and angle COD = 25° ; find the measure of:
(i) angle BOC
(ii) angle EOD
(iii) obtuse angle BOD
(iv) reflex angle BOD
(v) reflex angle COE.
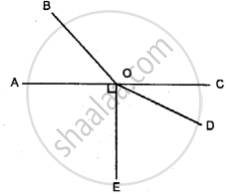
In the given figure, lines AB and CD intersect at point O.
(i) Find the value of ∠a.
(ii) Name all the pairs of vertically opposite angles.
(iii) Name all the pairs of adjacent angles.
(iv) Name all the reflex angles formed and write the measure of each.
Write the complement angle of: 45°
Write the complement angle of: (x – 10)°
Write the complement angle of: `2/5` of 70°
50% of 120°
`3/4` of 160°
The measures of two supplementary angles are (3x + 15)° and (2x + 5)°. Find x.
For an angle x°, find:
(i) the complementary angle
(ii) the supplementary angle
(iii) the value of x° if its supplementary angle is three times its complementary angle.
Find the angle formed by the arms of a clock at 3 O’clock.
