Advertisements
Advertisements
प्रश्न
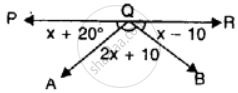
In the given figure, PQR is a straight line. Find x. Then complete the following:
(i) ∠AQB = _______
(ii) ∠BQP = _______
(iii) ∠AQR = _______
उत्तर
PQR is a straight line
∠AQP=x + 20°
∠AQB = 2x + 10°
∠BQR = x – 10°
But ∠AQP + ∠AQB + ∠BQR = 180°
⇒ x + 20° + 2x + 10° + x - 10°= 180°
⇒ 4x + 20°= 180°
⇒ 4x = 180° - 20°= 160°
⇒ x = `160^circ/4 = 40^circ`
(i) ∠AQB = 2x + 10° = 2 x 40° + 10° = 80° + 10° = 90°
∠AQP = x + 2(T = 40° + 20° = 60°
∠BQR = x – 10° = 40° – 10° = 30°
(ii) ∠BQP = ∠AQP + ∠AQB = 60° + 90° = 150°
(iii) ∠AQR = ∠AQB + ∠BQR = 90° + 30° = 120°
APPEARS IN
संबंधित प्रश्न
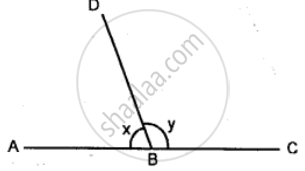
In the given diagram, ABC is a straight line. If x = 53°, find y.
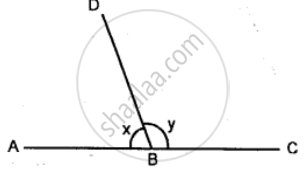
In the given diagram, ABC is a straight line. If y =`1 1/2` right angles; find x.
Write the complement angle of: (x – 10)°
Write the complement angle of: 20° + y°
Write the complement angle of: `1/5` of 160°
Write the complement angle of: `2/5` of 70°
Two supplementary angles are in the ratio 7 : 11. Find the angles.
The measures of two supplementary angles are (3x + 15)° and (2x + 5)°. Find x.
Find the angle formed by the arms of a clock at 9 O’clock.
For an angle y°, find:
(i) its supplementary angle.
(ii) its complementary angle.
(iii) the value of y° if its supplement is four times its complement.
