Advertisements
Advertisements
Question
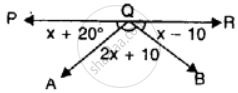
In the given figure, PQR is a straight line. Find x. Then complete the following:
(i) ∠AQB = _______
(ii) ∠BQP = _______
(iii) ∠AQR = _______
Solution
PQR is a straight line
∠AQP=x + 20°
∠AQB = 2x + 10°
∠BQR = x – 10°
But ∠AQP + ∠AQB + ∠BQR = 180°
⇒ x + 20° + 2x + 10° + x - 10°= 180°
⇒ 4x + 20°= 180°
⇒ 4x = 180° - 20°= 160°
⇒ x = `160^circ/4 = 40^circ`
(i) ∠AQB = 2x + 10° = 2 x 40° + 10° = 80° + 10° = 90°
∠AQP = x + 2(T = 40° + 20° = 60°
∠BQR = x – 10° = 40° – 10° = 30°
(ii) ∠BQP = ∠AQP + ∠AQB = 60° + 90° = 150°
(iii) ∠AQR = ∠AQB + ∠BQR = 90° + 30° = 120°
APPEARS IN
RELATED QUESTIONS
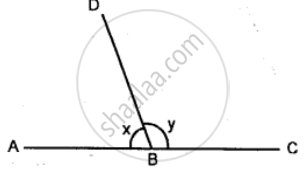
In the given diagram, ABC is a straight line. If y =`1 1/2` right angles; find x.
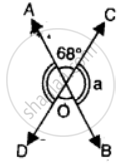
In the given figure, lines AB and CD intersect at point O.
(i) Find the value of ∠a.
(ii) Name all the pairs of vertically opposite angles.
(iii) Name all the pairs of adjacent angles.
(iv) Name all the reflex angles formed and write the measure of each.
Write the complement angle of: `1/5` of 160°
Write the complement angle of: `1/6` of 90°
`1/3` of 150°
The measures of two complementary angles are (2x – 7)° and (x + 4)°. Find x.
Explain what do you understand by complementary angles?
Find the angle formed by the arms of a clock at 3 O’clock.
Find the angle formed by the arms of a clock at 6 O’clock.
For an angle y°, find:
(i) its supplementary angle.
(ii) its complementary angle.
(iii) the value of y° if its supplement is four times its complement.
