Advertisements
Advertisements
Question
In the given figure, PQ is a mirror, AB is the incident ray and BC is the reflected ray. If ∠ABC = 46°, then ∠ABP is equal to ______.

Options
44°
67°
13°
62°
Solution
In the given figure, PQ is a mirror, AB is the incident ray and BC is the reflected ray. If ∠ABC = 46°, then ∠ABP is equal to 67°.
Explanation:
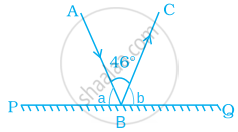
We know that, the angle of incidence is always equal to the angle of reflection.
∠ABP = ∠CBQ
i.e. a = b
Now, sum of all the angles on a straight line is 180°. .....[∵ ∠ABC = 46°, given]
∴ a + 46° + b = 180°
⇒ 2a = 180° – 46° .....[∵ a = b]
⇒ 2a = 134°
⇒ a = `134^circ/2` = 67°
∴ ∠ABP = 67°
APPEARS IN
RELATED QUESTIONS
Given that AB is a straight line. Calculate the value of x° in the following cases
Given that AB is a straight line. Calculate the value of x° in the following cases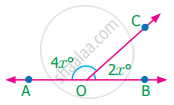
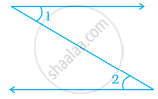
In the given figure the angles ∠1 and ∠2 are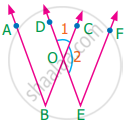
Using the figure, answer the following question and justify your answer
Does ∠BOC and ∠BOD form a linear pair?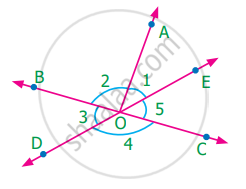
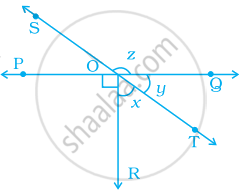
In the given figure, lines PQ and ST intersect at O. If ∠POR = 90° and x:y = 3:2, then z is equal to ______.
A linear pair may have two acute angles.
In the following figure, write, if any, (i) each pair of vertically opposite angles, and (ii) each linear pair.
Two angles are making a linear pair. If one of them is one-third of the other, find the angles.
