Advertisements
Advertisements
Question
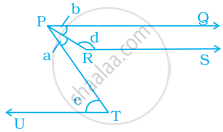
In the given figure, PQ, RS and UT are parallel lines. If c = 57° and a = `c/3`, find the value of d.
Solution
Since, PQ || UT and PT is transversal,
Therefore, ∠QPT = ∠UTP ......[Alternate interior angles]
⇒ a + b = c
⇒ `c/3` + b = c ......`[∵ a = c/3, "given"]`
⇒ b = `c - c/3`
⇒ b = `(3c - c)/3`
⇒ b = `(2c)/3 = 2/3 xx 57^circ` ......[∵ c = 57°, given]
∴ b = 38°
Again, PQ || RS and PR is transversal
Therefore, ∠QPR + ∠PRS = 180° ......[Consecutive interior angles]
⇒ b + d = 180°
⇒ d = 180° – b
⇒ d = 180° – 38° ......[∵ b = 38°]
⇒ d = 142°
APPEARS IN
RELATED QUESTIONS
Find the measure of angle x in the following figure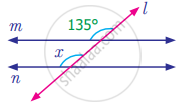
Find the measure of angle x in the following figure
Find the measure of angle y in the following figure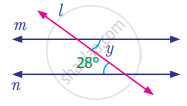
Find the measure of angle y in the following figure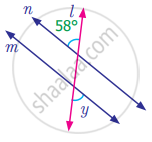
Anbu has marked the angles as shown in the following figure. Check whether it is correct. Give reason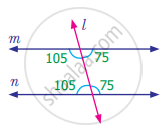
Find the value of z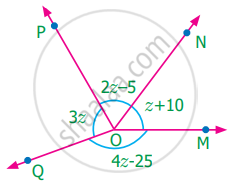
Find the value of x and y if RS is parallel to PQ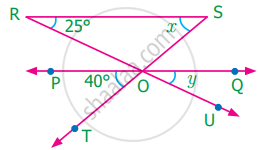
In the given figure, line l intersects two parallel lines PQ and RS. Then, which one of the following is not true?
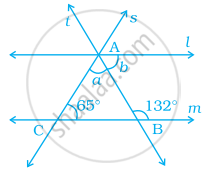
In the given figure, if l || m, find the values of a and b.
In the given figure, l || m and a line t intersects these lines at P and Q, respectively. Find the sum 2a + b.