Advertisements
Advertisements
Question
In the given figure, ∆PQR ≅ ∆ ______.
Solution
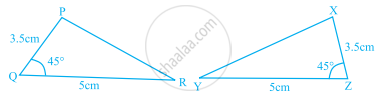
In the given figure, ∆PQR ≅ ∆XZY.
Explanation:

In ∆PQR and ∆XZY,
PQ = XZ = 3.5 cm
QR = ZY = 5 cm
∠PQR = ∠XZY = 45°
By SAS congruence criterion,
∆PQR ≅ ∆XZY
APPEARS IN
RELATED QUESTIONS
Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by using the SAS congruence rule. If the triangles are congruent, write them in symbolic form.
∆ABC, AB = 7 cm, BC = 5 cm, ∠B = 50°.
∆DEF, DE = 5 cm, EF = 7 cm, ∠E = 50°.
In Fig,
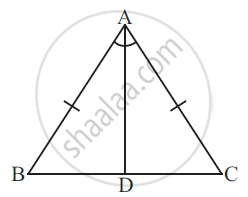
AB = AC and AD is the bisector of ∠BAC.
(i) State three pairs of equal parts in triangles ADB and ADC.
(ii) Is ∆ADB ≅ ∆ADC? Give reasons.
(iii) Is ∠B = ∠C? Give reasons.
For the given pair of triangles state the criterion that can be used to determine the congruency?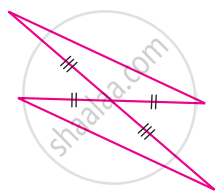
Construct a triangle ABC with given conditions.
AB = 7 cm, AC = 6.5 cm and ∠A = 120°
Construct a triangle PQR with given conditions.
∠P = 60°, ∠R = 35° and PR = 7.8 cm
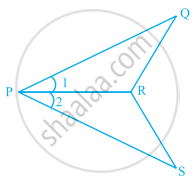
In the given figure, ΔPQR ≅ Δ ______.
In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.

In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.

State which of the following pairs of triangles are congruent. If yes, write them in symbolic form (you may draw a rough figure).
∆PQR: PQ = 3.5 cm, QR = 4.0 cm, ∠Q = 60°
∆STU: ST = 3.5 cm, TU = 4 cm, ∠T = 60°
In the given figure, PO = PS and ∠1 = ∠2.
- Is ∆PQR ≅ ∆PSR? Give reasons.
- Is QR = SR? Give reasons.