Advertisements
Advertisements
Question
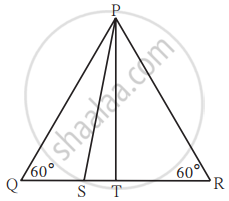
In the given figure, ∆PQR is an equilateral triangle. Point S is on seg QR such that QS = n\[\frac{1}{3}\] QR.
Prove that: 9 PS2 = 7 PQ2
Solution
Let the side of equilateral triangle ∆PQR be x.
PT be the altitude of the ∆PQR.
We know that, in equilateral triangle, altitude divides the base in two equal parts.
∴ QT = TR = \[\frac{1}{2}QR = \frac{x}{2}\]
Given: QS = \[\frac{1}{3}\] QR = \[\frac{x}{3}\]
\[\therefore ST = QT - QS = \frac{x}{2} - \frac{x}{3} = \frac{x}{6}\]
According to Pythagoras theorem,
In ∆PQT
\[{PQ}^2 = {QT}^2 + {PT}^2 \]
\[ \Rightarrow \left( x \right)^2 = \left( \frac{x}{2} \right)^2 + {PT}^2 \]
\[ \Rightarrow x^2 = \frac{x^2}{4} + {PT}^2 \]
\[ \Rightarrow {PT}^2 = x^2 - \frac{x^2}{4}\]
\[ \Rightarrow {PT}^2 = \frac{3 x^2}{4}\]
\[ \Rightarrow PT = \frac{\sqrt{3}x}{2}\]
In ∆PST \[{PS}^2 = {ST}^2 + {PT}^2 \]
\[ \Rightarrow {PS}^2 = \left( \frac{x}{6} \right)^2 + \left( \frac{\sqrt{3}x}{2} \right)^2 \]
\[ \Rightarrow {PS}^2 = \frac{x^2}{36} + \frac{3 x^2}{4}\]
\[ \Rightarrow {PS}^2 = \frac{x^2 + 27 x^2}{36}\]
\[ \Rightarrow {PS}^2 = \frac{28 x^2}{36}\]
\[ \Rightarrow {PS}^2 = \frac{7 x^2}{9}\]
\[ \Rightarrow 9 {PS}^2 = 7 {PQ}^2\]
Hence, 9 PS2 = 7 PQ2.
APPEARS IN
RELATED QUESTIONS
In the following figure, in ΔABC, ∠B = 90°, ∠C = 60°, ∠A = 30°, AC = 18 cm. Find BC.

Find the height of an equilateral triangle whose side is 6 units.
In the given figure. Find RP and PS using the information given in ∆PSR.

In right-angled triangle PQR, if ∠P = 60°, ∠R = 30° and PR = 12, then find the values of PQ and QR.
In ΔDEF, if ∠E = 90°, then find the value of ∠D + ∠F.
Choose the correct alternative:
Out of given triplets, which is a Pythagoras triplet?
Choose the correct alternative:
The diagonal of a square is `10sqrt(2)` cm then its perimeter is ______
From given figure, In ∆ABC, If ∠ABC = 90° ∠CAB=30°, AC = 14 then for finding value of AB and BC, complete the following activity.
Activity: In ∆ABC, If ∠ABC = 90°, ∠CAB=30°
∴ ∠BCA = `square`
By theorem of 30° – 60° – 90° triangle,
∴ `square = 1/2` AC and `square = sqrt(3)/2` AC
∴ BC = `1/2 xx square` and AB = `sqrt(3)/2 xx 14`
∴ BC = 7 and AB = `7sqrt(3)`
From given figure, in ∆MNK, if ∠MNK = 90°, ∠M = 45°, MK = 6, then for finding value of MN and KN, complete the following activity.
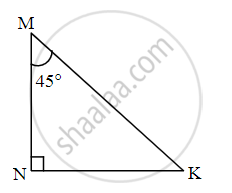
Activity:
In ∆MNK, ∠MNK = 90°, ∠M = 45° …...[Given]
∴ ∠K = `square` .....[Remaining angle of ∆MNK]
By theorem of 45° – 45° – 90° triangle,
∴ `square = 1/sqrt(2)` MK and `square = 1/sqrt(2)` MK
∴ MN = `1/sqrt(2) xx square` and KN = `1/sqrt(2) xx 6`
∴ MN = `3sqrt(2)` and KN = `3sqrt(2)`
From the given figure, in ∆ABC, if AD ⊥ BC, ∠C = 45°, AC = `8sqrt(2)` , BD = 5, then for finding value of AD and BC, complete the following activity.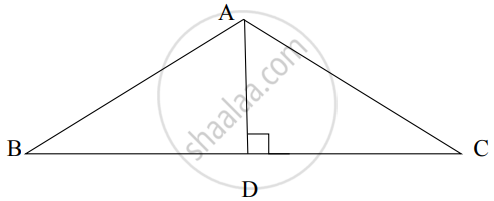
Activity: In ∆ADC, if ∠ADC = 90°, ∠C = 45° ......[Given]
∴ ∠DAC = `square` .....[Remaining angle of ∆ADC]
By theorem of 45° – 45° – 90° triangle,
∴ `square = 1/sqrt(2)` AC and `square = 1/sqrt(2)` AC
∴ AD =`1/sqrt(2) xx square` and DC = `1/sqrt(2) xx 8sqrt(2)`
∴ AD = 8 and DC = 8
∴ BC = BD +DC
= 5 + 8
= 13
As shown in figure, LK = `6sqrt(2)` then

- MK = ?
- ML = ?
- MN = ?
In ∆RST, ∠S = 90°, ∠T = 30°, RT = 12 cm, then find RS.
