Advertisements
Advertisements
Question
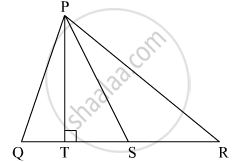
In the given figure, seg PS is the median of ∆PQR and PT ⊥ QR. Prove that,
PQ2 = PS2 − QR × ST + `(("QR")/2)^2`
Sum
Solution
Seg PS is the median of ∆PQR ...(Given)
∴ QS = SR = `1/2`QR ...(1) [S is the midpoint of side QR]
In ∆PTS, ∠PTS = 90° ...(Given)
∴ by Pythagoras theorem,
PS2 = PT2 + TS2 ...(2)
In ∆PTQ, ∠PTQ = 90° ...(Given)
∴ by Pythagoras theorem,
PQ2 = PT2 + TQ2
∴ PQ2 = PT2 + (QS − TS)2 ...(Q - T - S)
∴ PQ2 = PT2 + QS2 − 2QS × TS + TS2 ...[(a − b)2 = a2 − 2ab + b2]
∴ PQ2 = (PT2 + TS2) − 2QS × TS + QS2
∴ PQ2 = PS2 − 2`(("QR")/2)` × TS + `(("QR")/2)^2` ...[From (1) and (2)]
∴ PQ2 = PS2 − QR × ST + `(("QR")/2)^2`
shaalaa.com
Is there an error in this question or solution?
