Advertisements
Advertisements
Question
In the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that :
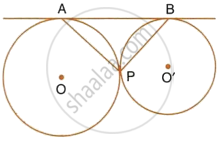
- tangent at point P bisects AB,
- angles APB = 90°.
Solution
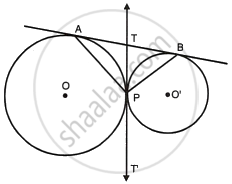
Draw TPT' as common tangent to the circles.
i. TA and TP are the tangents to the circle with centre O.
Therefore, TA = TP ...(i)
Similarly, TP = TB ...(ii)
From (i) and (ii)
TA = TB
Therefore, TPT' is the bisector of AB.
ii. Now in ΔATP,
∴ ∠TAP = ∠TPA
Similarly in ΔBTP, ∠TBP = ∠TPB
Adding,
∠TAP +∠TBP = ∠APB
But
∴ TAP + ∠TBP + ∠APB = 180°
`=>` ∠APB = ∠TAP + ∠TBP = 90°
APPEARS IN
RELATED QUESTIONS
Two circle touch each other internally. Show that the tangents drawn to the two circles from any point on the common tangent are equal in length.
Two parallel tangents of a circle meet a third tangent at points P and Q. Prove that PQ subtends a right angle at the centre.
Two circles intersect at P and Q. Through P, a straight line APB is drawn to meet the circles in A and B. Through Q, a straight line is drawn to meet the circles at C and D. Prove that AC is parallel to BD.
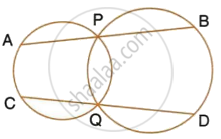
Two circles intersect each other at points A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.
In the figure, given below, AC is a transverse common tangent to two circles with centres P and Q and of radii 6 cm and 3 cm respectively.
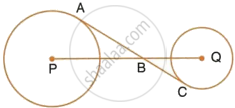
Given that AB = 8 cm, calculate PQ.
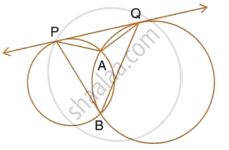
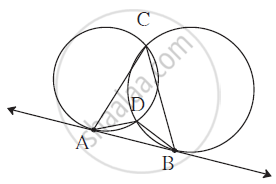
Two circles intersect each other at points C and D. Their common tangent AB touches the circles at point A and B. Prove that :
∠ ADB + ∠ ACB = 180°
In which qudrant does point A(-3, 2) lie?
On which axis does point B(12, 0) lie?
Two circles of radii 5cm and 3cm with centres O and P touch each other internally. If the perpendicular bisector of the line segment OP meets the circumference of the larger circle at A and B, find the length of AB.
P and Q are the centre of circles of radius 9 cm and 2 cm respectively; PQ = 17 cm. R is the centre of circle of radius x cm, which touches the above circles externally, given that ∠ PRQ = 90°. Write an equation in x and solve it.
Two circles with centres O and O' touch each other at point L. Prove that, a tangent through L bisects the common tangent AB of the two circles at point M.
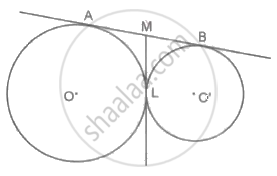
Given: AB is a common tangent of the two circles that touch each other at point L. ML is a tangent through point L.
To prove: M is a mid-point of the tangent AB or MA = MB.
Proof: From the figure,
M is an external point that draws two tangents, MA and ML to the circle with the centre O.
So, `square` = `square` ......(i)
Similarly, M draws two tangents ML and MB to the circle with the centre O'.
So, `square` = `square` ......(ii)
From the equations (i) and (ii),
`square` = `square`
Hence, the tangent at the point L, bisects the common tangent, AB of the two circles at point M.
