Advertisements
Advertisements
Question
केंद्र C और त्रिज्या 3.4 सेमी लेकर एक वृत्त खींचिए। इसकी कोई जीवा `overline"AB"` खींचिए। इस जिवा `overline"AB"` का लंब समद्विभाजक खींचिए। जाँच कीजिए कि क्या यह वृत्त के केंद्र C से होकर जाता है।
Solution
-
शीट पर कोई भी बिन्दु C अंकित करें।
-
परकार को 3.4 सेमी तक समायोजित करके और परकार के सूचक को बिंदु C पर रखकर, परकार को धीरे-धीरे घुमाकर वृत्त बनाएं। यह 3.4 सेमी त्रिज्या का अभीष्ट वृत्त है।
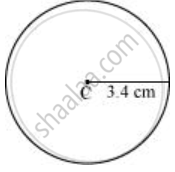
- अब, वृत्त में किसी भी तार को `overline"AB"` चिह्नित करें।
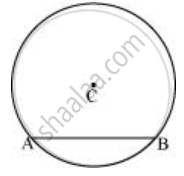
- A और B को केंद्र मानकर `overline"AB"` के दोनों ओर चाप बनाएं। माना कि ये एक दूसरे को D और E पर काटते हैं।
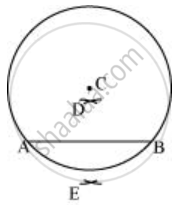
-
DE से जुड़ें, जो AB का लम्ब समद्विभाजक है।
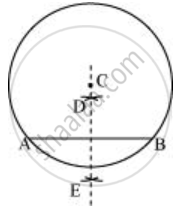
जब `overline"DE"` को बढ़ाया जाता है, तो यह बिंदु C से होकर गुजरेगा।
APPEARS IN
RELATED QUESTIONS
एक रेखाखंड `overline"XY"` का लंब समद्विभाजक खींचिए जिसकी लंबाई 10.3 सेमी है।
- इस लंब समद्विभाजक पर कोई बिंदु P लीजिए। जाँच कीजिए कि PX = PY है।
- यदी M रेखाखंड `overline"XY"` का मध्य बींदु है, तो MX और XY के विषय में आप क्या कह सकते हैं?
लंबाई 12.8 सेमी वाला एक रेखाखंड खींचिए। रूलर और परकार की सहायता से इसके चार बराबर भाग कौजिए। मापन द्वारा अपनी रचना की जाँच कीजिए।
4 सभी ज्रिज्या का एक वृत्त खोचिए। इसका काई दो जीवाएँ खांचिए। इन दोनों जीवाओं के लंब समद्रिभाजक खींचिए। ये कहाँ मिलते हैं?
शीर्ष O वाला कोई कोण खींचिए। इसकी एक भुजा पर एक बिंदु A और दूसरी भुजा पर एक अन्य बिंदु B इस परकार लीजिए कि OA = OB है। OA और OB के लंब समद्विभाजक खींचिए। मान लीजिए ये P पर प्रतिछेदित करते हैं क्या PA = PB है?
