Advertisements
Advertisements
Question
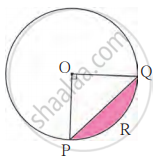
केंद्र O असलेल्या वर्तुळात PQ ही जीवा आहे. ∠POQ = 90°, आणि छायांकित भागाचे क्षेत्रफळ 114 चौसेमी आहे, तर वर्तुळाची त्रिज्या काढा. (π = 3.14)
Solution
दिलेले: केंद्रीय कोन (θ) = ∠POQ = 90°
A(वर्तुळखंड PRQ) = 114 सेमी2
शोधा: त्रिज्या (r)
उकल:
A(वर्तुळखंड PRQ) = r2 `[(piθ)/360 - sinθ/2]`
∴ 114 = `r^2[(3.14 xx 90)/360 - (sin90°)/2]`
∴ `114 = r^2[3.14/4 - 1/2]`
∴ `114 = r^2[3.14/4 - (1 xx 2)/(2 xx 2)]`
∴ `114 = r^2[3.14/4 - 2/4]`
∴ `114 = r^2[(3.14 - 2)/4]`
∴ `114 = r^2 xx 1.14/4`
∴ `r^2 = (114 xx 4)/1.14`
∴ `r^2 = (11400 xx 4)/114`
∴ `r^2 = 100 xx 4`
∴ r = 10 × 2 ....[दोन्ही बाजूंचे वर्गमूळ घेऊन]
∴ r = 20 सेमी
∴ दिलेल्या वर्तुळाची त्रिज्या 20 सेमी आहे.
APPEARS IN
RELATED QUESTIONS
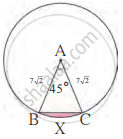
आकृतीमध्ये A केंद्र असलेल्या वर्तुळात ∠ABC = 45°, AC = `7sqrt2` सेमी, तर वर्तुळखंड BXC चे क्षेत्रफळ काढा. (π = 3.14, `sqrt2` = 1.41)
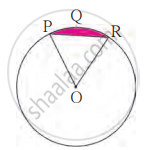
आकृती मध्ये O हे वर्तुळकेंद्र आहे. m(कंस PQR) = 60°, OP = 10 सेमी, तर छायांकित भागाचे क्षेत्रफळ काढा. (π = 3.14, `sqrt3` = 1.73)
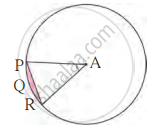
A केंद्र असलेल्या वर्तुळात ∠PAR = 30° AP = 7.5 तर, वर्तुळखंड PQR चे क्षेत्रफळ काढा. (π = 3.14)