Advertisements
Advertisements
Question
किसी मैदान को समतल करने के लिए 120 सेमी व्यास तथा 84 सेमी लंबाई वाले रोलर के 200 फेरे लगते हैं, तो 10 रु प्रतिवर्ग मीटर की दर से मैदान समतल करने में कितना खर्च लगेगा?
Solution
रोलर का व्यास = 120 सेमी
∴ उसकी त्रिज्या (r) = `120/2 = 60` सेमी
उसकी लंबाई (h) = 84 सेमी
रोलर का वक्रपृष्टफल = 2πrh
= `2 xx 22/7 xx 60 xx 84 = 31680` सेमी2
= `31680/10000` मी2 .............(1 मी2 = 10000 सेमी2)
एक फेरे में रोलर द्वारा समतल हुई जगह का क्षेत्रफल 3.168 मी2 है |
∴ 200 फेरे में रोलर द्वारा समतल हुई जगह का क्षेत्रफल
= 200 × 3.168 = 633.6 मी2
प्रति वर्गमीटर की दर से समतल करने का खर्च ₹ 10 है |
∴ मैदान समतल करने में लगा कुल खर्च = 633.6 × 10
= ₹ 6336
मैदान समतल करने में कुल खर्च ₹ 6336 लगेगा |
APPEARS IN
RELATED QUESTIONS
नीचे दिए गए बहुवैकल्पिक प्रश्न में से उचित विकल्प चुनकर लिखिए।
5 सेमी त्रिज्या वाले किसी लंबवृत्ताकार बेलन का वक्रपृष्ठफल 440 सेमी2 हो तो उस लंबवृत्ताकार बेलन की ऊँचाई कितनी होगी?
नीचे दिए गए बहुवैकल्पिक प्रश्न में से उचित विकल्प चुनकर लिखिए।
किसी शंकु को पिघलाकर उसके आधार की त्रिज्या के बराबर त्रिज्या वाला लंबवृत्ताकार बेलन बनाया गया। यदि लंबवृत्ताकार बेलन की ऊँचाई 5 सेमी हो तो शंकु की ऊँचाई कितनी होगी?
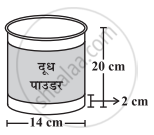
एक कंपनी अपने दूध पाउडर को ऐसे बेलनाकार बर्तनों में पैक करती है जिनका व्यास 14 cm और ऊँचाई 20 cm है। कंपनी बर्तन के पृष्ठ के चारों ओर एक लेबल लगाती है (जैसा कि आकृति में दर्शया गया है)। यदि यह लेबल बर्तन के तल और शीर्ष दोनों से 2 cm की दूरी पर चिपकाया जाता है तो लेबल का क्षेत्रफल क्या है?
यदि एक बेलन की त्रिज्या दोगुनी कर दी जाए और ऊँचाई आधी कर दी जाए, तो इसका वक्र पृष्ठीय क्षेत्रफल ______ होगा।
दो बेलनों की त्रिज्याएँ 2 : 3 के अनुपात में हैं तथा उनकी ऊँचाईयों का अनुपात 5 : 3 है। उनके आयतनों का अनुपात है
10 m × 10 m × 5 m विमाओं वाले एक कमरे में रखे जा सकने वाले सबसे लंबे डंडे की लंबाई है
यदि एक बेलन की त्रिज्या दुगुनी कर दी जाए तथा उसके वक्र पृष्ठीय क्षेत्रफल में कोई परिवर्तन न किया जाए, तो उसकी ऊँचाई अवश्य ही आधी हो जाएगी।
यदि एक बेलन की त्रिज्या दुगुनी कर दी जाए और उसकी ऊँचाई आधी कर दी जाए, तो उसका आयतन दुगुना हो जाएगा।
दोनों ओर से खुली एक बेलनाकार ट्यूब एक लोहे की चादर की बनी है जिसकी मोटाई 2 cm है। यदि इसका व्यास 16 cm और लंबाई 100 cm है तो ज्ञात कीजिए कि इस ट्यूब के बनाने में कितने cm3 लोहे का प्रयोग किया गया है।
वृत्ताकार लंब बेलन का वक्र पृष्ठफल 1980 सेमी2 है और आधार की त्रिज्या 15 सेमी तो उस वृत्ताकार लंब बेलन की ऊँचाई ज्ञात कीजिए। (π = `22/7`)
