Advertisements
Advertisements
Question
किसी त्रिभुज की परिमिति 14.4 सेमी है और भुजाओं का अनुपात 2 : 3 : 4 हो, तो त्रिभुज की रचना कीजिए।
Solution 1
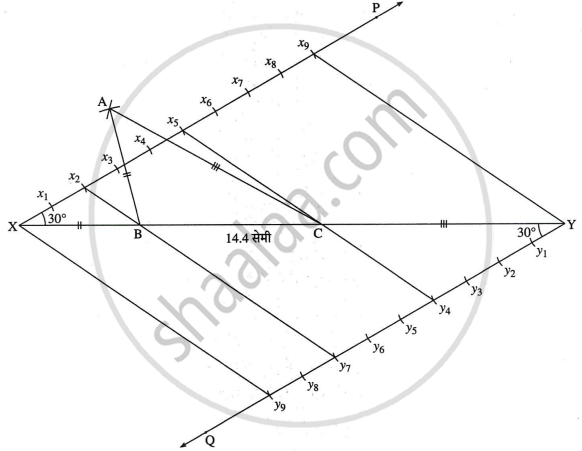
स्पष्टीकरण:
मानो ΔABC अभीष्ट त्रिभुज है।
रेख XY = 14.4 सेमी खींचो, जो ΔABC की परिमिति है।
हमे रेख XY को 2ः3ः4 के अनुपात मे विभाजित करना है।
किरण XP इस प्रकार खींचो कि, `angle`YXP = 30°
किरण XP की विपरीत ओर रेख YQ इस प्रकार खींचो कि, `angle`XYQ = 30°
किरण XP के 9 समान भाग अर्थात बनाओ `X_(x_1)`, x1x2, ... ,x8x9 बनाओ।
इसी प्रकार आकृति के अनुसार, किरण YQ के 9 समान भाग बनाओ।
x2y7 तथा x5y4 को मिलाओ, जो रेख XY को क्रमश B तथा C पर प्रतिच्छेदित करती हैं।
B को केंद्र तथा BX को त्रिज्या मानकर चाप खींचो।
C को केंद्र तथा CY को त्रिज्या मानकर चाप खींचो, जो पहले चाप को बिंदु A पर प्रतिच्छेदित करता है।
रेख AB तथा रेख AC खींचो।
ΔABC अभीष्ट त्रिभुज है।
Solution 2
कच्ची आकृति:
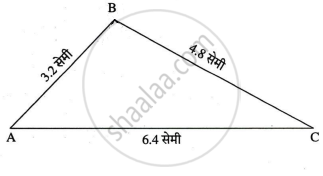
स्पष्टीकरण:
मानो, ABC दिया त्रिभुज है।
AB = BC = AC = 2 : 3 : 4
∴ AB = 2x सेमी, BC = 3x सेमी, AC = 4x सेमी ...(x सामान्य गुणज हैं।)
ΔABC की परिमिति = 14.4 सेमी
∴ AB + BC + AC= 14.4
∴ 2x + 3x + 4x = 14.4
∴ 9x = 14.4
∴ `x = 14.4/9`
∴ x = 1.6
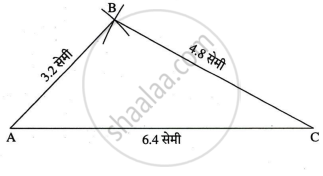
AB = 2x = `2 xx 1.6` = 3.2 सेमी
BC = 3x = `3 xx 1.6` = 4.8 सेमी
AC = 4x = `4 xx 1.6` = 6.4 सेमी