Advertisements
Advertisements
Question
कथन “प्रत्येक रेखा l और उस पर न स्थित प्रत्येक बिंदु P के लिए, एक अद्वितीय रेखा का अस्तित्व है जो P से होकर जाती है और l के समांतर है” प्लेफेयर अभिगृहीत कहलाता है।
Options
सत्य
असत्य
Solution
यह कथन सत्य है।
स्पष्टीकरण -
दिया गया कथन यूक्लिड की पाँचवीं अभिधारणा का समतुल्य संस्करण है और इसे प्लेफेयर की अभिगृहीत के रूप में जाना जाता है।
APPEARS IN
RELATED QUESTIONS
निम्नलिखित कथन सत्य हैं या असत्य हैं? अपने उत्तर के लिए कारण दीजिए।
यदि दो वृत्त बराबर हैं, तो उनकी त्रिज्याएँ बराबर होती हैं।
निम्नलिखित पद की परिभाषा दीजिए। क्या इनके लिए कुछ ऐसे पद हैं, जिन्हें परिभाषित करने की आवश्यकता है? वे क्या हैं और आप इन्हें कैसे परिभाषित कर पाएँगे?
वर्ग
निम्नलिखित में से किसको उपपत्ति की आवश्यकता है?
यूक्लिड के कथन, सभी समकोण एक दूसरे के बराबर होते हैं, निम्नलिखित के रूप में दिया गया है :
यूक्लिडीय ज्यामिति केवल वक्र पृष्ठों के लिए ही मान्य है।
एक पृष्ठ के किनारे वक्र होते हैं।
यदि एक राशि B एक अन्य राशि A का एक भाग है, तो A को B और एक अन्य राशि C के योग के रूप में लिखा जा सकता है।
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
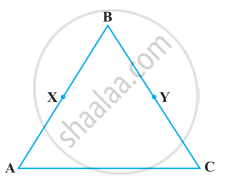
निम्नलिखित आकृति में, हमें प्राप्त है :
BX = `1/2` AB, BY = `1/2` BC तथा AB = BC है। दर्शाइए कि BX = BY है।
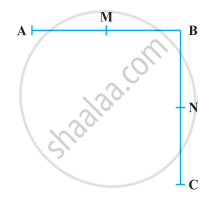
निम्नलिखित आकृति में AB = BC, M रेखाखंड AB का मध्य-बिंदु है और N रेखाखंड BC का मध्य-बिंदु है। दर्शाइए कि AM = NC है।
निम्नलिखित कथन को पढ़िए :
एक समबाहु त्रिभुज तीन रेखाखंडों से बना एक बहुभुज है जिनमें से दो रेखाखंड तीसरे रेखाखंड के बराबर हैं तथा इसका प्रत्येक कोण 60° का है।
इस परिभाषा में, उन पदों को परिभाषित कीजिए जिन्हें आप आवश्यक समझते हैं। क्या इसमें कोई अपरिभाषित पद है? क्या आप इसका औचित्य दे सकते हैं कि एक समबाहु त्रिभुज के सभी कोण और सभी भुजाएँ बराबर होती हैं।
