Advertisements
Advertisements
Question
Let an electromagnetic wave propagate along the x-direction, the magnetic field oscillates at a frequency of 1010 Hz and has an amplitude of 10-5 T, acting along the y – direction. Then, compute the wavelength of the wave. Also write down the expression for the electric field in this case.
Solution
Frequency of electromagnetic wave, v = 1010 Hz
Amplitude of Oscillating magnetic field, B0 = 10-5 T
Wave length of the wave, λ = `"C"/"f" = (3 xx 10^8)/10^10 = 3 xx 10^-2`m
Amplitude of oscillating electric field, E0 = B0 C
C = `"E"_0/"B"_0`
E0 = 10-5 × 3 × 108
E0 = 3 × 103 = NC-1
Experession for the electric field in Oscillating wave
E = E0 sin (kx -wt)
K = `(2pi)/lambda = (2 xx 3.14)/(3 xx 10^-2) = 209 xx 10^2`
W = 2πƒ = 2 × 3.14 x 1010 = 6.28 × 1010
`vec"E"` = 3 x 103 sin (2.09 × 102 x – 6.28 × 1010 t) `hat"i"` NC-1.
APPEARS IN
RELATED QUESTIONS
About 5% of the power of a 100 W light bulb is converted to visible radiation. What is the average intensity of visible radiation
(a) at a distance of 1 m from the bulb?
(b) at a distance of 10 m?
Assume that the radiation is emitted isotropically and neglect reflection.
Which segment of electromagnetic waves has highest frequency? How are these waves produced? Give one use of these waves.
If the amplitude of the magnetic field is 3 x 10-6 T, then amplitude of the electric field for a electromagnetic waves is ______.
Which of the following is an electromagnetic wave?
Let E = E0 sin[106 x -ωt] be the electric field of plane electromagnetic wave, the value of ω is ______.
A transmitter consists of LC circuit with an inductance of 1 μH and a capacitance of 1 μF. What is the wavelength of the electromagnetic waves it emits?
Maxwell's equation describe the fundamental law of
Show that the radiation pressure exerted by an EM wave of intensity I on a surface kept in vacuum is I/c.
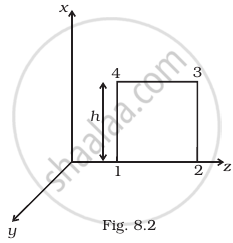
A plane EM wave travelling in vacuum along z direction is given by `E = E_0 sin(kz - ωt)hati` and `B = B_0 sin(kz - ωt)hatj`
- Evaluate `oint E.dl` over the rectangular loop 1234 shown in figure.
- Evaluate `int B.ds` over the surface bounded by loop 1234.
- Use equation `oint E.dl = (-dphi_B)/(dt)` to prove `E_0/B_0` = c.
- By using similar process and the equation `ointB.dl = mu_0I + ε_0 (dphi_E)/(dt)`, prove that c = `1/sqrt(mu_0ε_0)`
A plane electromagnetic wave of frequency 500 MHz is travelling in a vacuum along a y-direction.
At a particular point in space and time, `vec"B"` = 8.0 × 10-8 `hat"Z"`T. The value of the electric field at this point is ______.
(speed of light = 3 × 108 ms-1)
`hat x, hat y, hat z` are unit vectors along x, y, and Z directions.
