Advertisements
Advertisements
Question
Monica has a piece of Canvas whose area is 551 m2. She uses it to have a conical tent made, with a base radius of 7m. Assuming that all the stitching margins and wastage incurred while cutting, amounts to approximately 1 m2. Find the volume of the tent that can be made with it.
Solution
Given that,
Area of canvas ` 551m^2` and area of the canvas lost in wastage is `1m^2`
∴ area of canvas available for making the tent is `(551-1)m^2=550m^2.`
SA of tent =`550m^2` required base radius of conical tent= 7m
CSA of tent=`550m^2 `
`pirl=550m^2`
`⇒22/7xx7xxl=550`
`⇒l=550/22=25m `
Now, WKT
`l^2=r^2+h^2`
`⇒(25)^2-(7)^2=h^2 `
`⇒ h=sqrt(625-49)`
`=sqrt576=24m`
So, the volume of the conical tent =`1/3pir^2h`
`= 1/3xx3.14xx(7xx7)(24)m^3=1232m^3`
APPEARS IN
RELATED QUESTIONS
Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find
- radius of the base and
- total surface area of the cone.
`["Assume "pi =22/7]`
A joker’s cap is in the form of right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
`["Assume "pi=22/7]`
The area of the curved surface of a cone is 60 cm2. If the slant height of the cone be 8 cm, find the radius of the base?
The curved surface area of a cone is 12320 cm2. If the radius of its base is 56 cm, find its height.
A cone of height 15 cm and diameter 7 cm is mounted on a hemisphere of same diameter. Determine the volume of the solid thus formed.
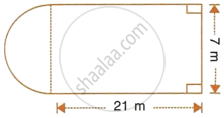
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.
What will be the cost of making a closed cone of tin sheet having radius of base 6 m and slant height 8 m if the rate of making is Rs.10 per sq.m? `(π = 22/7)`
Total surface area of a cone is 616 sq.cm. If the slant height of the cone is three times the radius of its base, find its slant height.
A sphere and a cone have the same radii. If their volumes are also equal, prove that the height of the cone is twice its radius.
The total surface area of a right circular cone of slant height 13 cm is 90π cm2. Calculate: its volume in cm3. Take π = 3.14
