Advertisements
Advertisements
Question
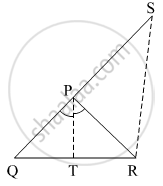
निचे दी गई आकृति के आधार पर रेख PT यह ∠QPR की समद्विभाजक है। बिंदु R से रेख PT के समांतर खींची गई रेखा, किरण QP को बिंदु S पर प्रतिच्छेदित करती हैतो सिद्ध कीजिए कि PS = PR
Solution
दिया गया है : किरण PT, ∠QPR का समद्विभाजक है।
साध्य : PS = PR
निर्माण : रेख PT || रेख SR
उपपत्ति :
किरण PT, ∠QPR का समद्विभाजक है। ...[दिया गया]
∴ ∠QPT = ∠RPT ….(i)
रेख PT || रेख SR
तथा रेखा QS इनकी तिर्यक रेखा है।
∴ ∠QPT = ∠PSR ....(ii) ...[संगत कोण]
रेख PT || रेख SR
तथा रेखा PR इनकी तिर्यक रेखा है।
∴ ∠RPT = ∠PRS ...(iii) [एकांतर कोण]
∴ ∠PRS = ∠PSR ...(iv) [(i), (ii) तथा (3) से]
∆PSR में,
∠PRS = ∠PSR ...[(iv) से]
∴ PS = PR ...[समद्विबाहु त्रिभुज के प्रमेय से]
APPEARS IN
RELATED QUESTIONS
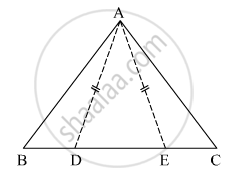
आकृति में Δ ABC की भुजा BC पर बिंदु D तथा E इस प्रकार हैं कि BD = CE तथा AD = AE तो सिद्ध कीजिए कि Δ ABD ≅ ΔACE
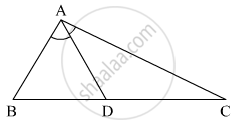
आकृति में, ΔABC के कोण ∠BAC की समद्विभाजक BC को बिंदु D पर प्रतिच्छेदित करती है तो सिदध् कीजिए कि AB > BD
निचे दी गई आकृति के आधार पर रेख AD ⊥ रेख BC रेख AE, यह ∠CAB का समद्विभाजक है। E-D-C है
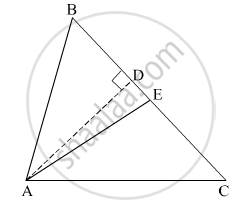
सिद्ध कीजिए ∠DAE = `1/2` (m∠C - m∠B)
