Advertisements
Advertisements
Question
नीचे दी हुई दो अभिधरणाओं पर विचार कीजिए:
- दो भिन्न बिंदु A और B दिए रहने पर, एक तीसरा बिंदु C ऐसा विद्यमान है जो A और B के बीच स्थित होता है।
- यहाँ कम से कम ऐसे तीन बिंदु विद्यमान हैं कि वे एक रेखा पर स्थित नहीं हैं।
Solution
हाँ, इन अभिधारणाओं में 'बिंदु और रेखा' जैसे अपरिभाषित शब्द शामिल हैं। साथ ही, ये अभिधारणाएँ अविरोधी हैं क्योंकि वे दो भिन्न स्थितियों से निपटती हैं जैसे
- यह बताता है कि दो बिंदु A और B दिए जाने पर, उन्हें जोड़ने वाली रेखा पर एक बिंदु C स्थित होता है। जबकि
- यह कहा गया है कि दिए गए बिंदु A और B में से आप एक बिंदु C का चयन कर सकते हैं जो उन्हें जोड़ने वाली रेखा पर नहीं है।
नहीं, ये अभिधारणाएँ यूक्लिड की अभिधारणाओं से अनुसरण नहीं करती हैं, हालाँकि वे इस स्वयंसिद्ध से अनुसरण करती हैं, "दो भिन्न बिंदु दिए गए हैं, एक अद्वितीय रेखा है जो इनसे होकर गुजरती है।"
APPEARS IN
RELATED QUESTIONS
निम्नलिखित कथन सत्य हैं या असत्य हैं? अपने उत्तर के लिए कारण दीजिए।
यदि दो वृत्त बराबर हैं, तो उनकी त्रिज्याएँ बराबर होती हैं।
आकृति में, यदि AC = BD है, तो सिद्ध कीजिए कि AB = CD है।

निम्नलिखित में से किसको उपपत्ति की आवश्यकता है?
एक पृष्ठ के किनारे वक्र होते हैं।
वस्तुएँ जो एक ही वस्तु की दोगुनी हों परस्पर बराबर होती हैं।
दो भिन्न प्रतिच्छेदी रेखाएँ एक ही रेखा के समांतर नहीं हो सकतीं।
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
निम्नलिखित आकृति में, ∠ABC = ∠ACB और ∠3 = ∠4 है। दर्शाइए कि ∠1 = ∠2 है।
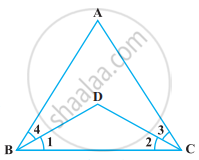
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
निम्नलिखित आकृति में, यदि OX = `1/2` XY, PX = `1/2` XZ और OX = PX हो, तो दर्शाइए कि XY = XZ है।
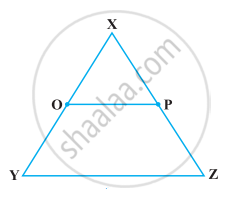
निम्नलिखित आकृति में BM = BN हैं, M रेखाखंड AB का मध्य-बिंदु है तथा N रेखाखंड BC का मध्य-बिंदु है। दर्शाइए कि AB = BC है।

निम्नलिखित कथन का अध्ययन कीजिए :
“दो प्रतिच्छेदी रेखाएँ एक ही रेखा पर लंब नहीं हो सकती हैं।”
जाँच कीजिए कि क्या यह कथन यूक्लिड पाँचवीं अभिधारणा का समतुल्य रूपांतरण है।
[संकेत : उपरोक्त कथन में, दो प्रतिच्छेदी रेखा l और m तथा एक अन्य रेखा n की पहचान कीजिए।]
