Advertisements
Advertisements
Question
यदि दो बिंदुओं A और B के बीच एक बिंदु C ऐसा स्थित है कि AC = BC है, तो सिद्ध कीजिए कि AC = `1/2` AB है। एक आकृति खींच कर इसे स्पष्ट कीजिए।
Solution
दिया जाता है कि,
AC = BC

AC + AC = BC + AC ...(दोनों पक्षों में समान जोड़ दिए जाते हैं) ...(1)
यहाँ, (BC + AC) AB के साथ संपाती है। यह ज्ञात है कि जो चीजें एक दूसरे के साथ मेल खाती हैं वे एक दूसरे के समान होती हैं।
∴ BC + AC = AB …(2)
यह भी ज्ञात है कि जो चीजें एक ही चीज के समान होती हैं वे एक दूसरे के समान होती हैं। इसलिए, समीकरण (1) और (2) से, हम प्राप्त करते हैं
AC + AC = AB
2AC = AB
∴ AC = `1/2 AB`
APPEARS IN
RELATED QUESTIONS
निम्नलिखित कथन सत्य हैं या असत्य हैं? अपने उत्तर के लिए कारण दीजिए।
दो भिन्न बिंदुओं से होकर जाने वाली असंख्य रेखाएँ हैं।
निम्नलिखित कथन सत्य हैं या असत्य हैं? अपने उत्तर के लिए कारण दीजिए।
आकृति में, यदि AB = PQ और PQ = XY, तो AB = XY होगा।

प्राचीन भारत में, आयतों, त्रिभुजों और समलंबों से संयोजित आकारों की वेदियाँ निम्नलिखित में प्रयोग होती थीं :
यूक्लिड निम्नलिखित देश का वासी था :
कथन “प्रत्येक रेखा l और उस पर न स्थित प्रत्येक बिंदु P के लिए, एक अद्वितीय रेखा का अस्तित्व है जो P से होकर जाती है और l के समांतर है” प्लेफेयर अभिगृहीत कहलाता है।
यूक्लिड की पाँचवीं अभिधारणा को अन्य अभिधारणाओं और अभिगृहीतों का प्रयोग करते हुए, सिद्ध करने के प्रयासों के फलस्वरूप अन्य अनेक ज्यामितियों की खोज हुई।
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
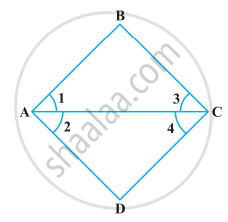
निम्नलिखित आकृति में, हमें प्राप्त है :
BX = `1/2` AB, BY = `1/2` BC तथा AB = BC है। दर्शाइए कि BX = BY है।
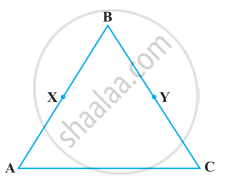
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
निम्नलिखित आकृति में, ∠1 = ∠3 और ∠2 = ∠4 है। दर्शाइए कि ∠A = ∠C है।
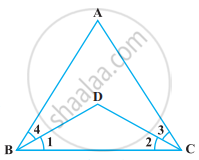
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
निम्नलिखित आकृति में, ∠ABC = ∠ACB और ∠3 = ∠4 है। दर्शाइए कि ∠1 = ∠2 है।
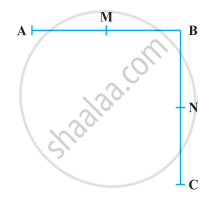
निम्नलिखित आकृति में AB = BC, M रेखाखंड AB का मध्य-बिंदु है और N रेखाखंड BC का मध्य-बिंदु है। दर्शाइए कि AM = NC है।