Advertisements
Advertisements
Question
निम्नांकित प्रश्न का सत्यापन कीजिए -
(a – b)(a – b)(a – b) = a3 – 3a2b + 3ab2 – b3
Solution
ध्यान दें कि दिए गए व्यंजक है,
चूंकि, हमें सत्यापित करना है,
(a – b)(a – b)(a – b) = a3 – 3a2b + 3ab2 – b3
जहां,
L.H.S. = (a − b)(a − b)(a − b)
L.H.S. का मूल्यांकन करें,
= (a − b)(a − b)(a − b)
= (a – b)(a – b)2
= (a − b)(a2 + b2 − 2ab)
= a(a2 + b2 − 2ab) + b(a2 + b2 − 2ab)
= a3 + ab2 − 2a2b + a2b + b3 − 2ab2
= a3 – 3a2b + 3ab2 – b3
= R.H.S.
APPEARS IN
RELATED QUESTIONS
उपयुक्त सर्वसमिकाओं का प्रयोग करते हुए, निम्न को प्रसारित कीजिए -
(xy + yz)2
उपयुक्त सर्वसमिकाओं का प्रयोग करते हुए, निम्न को प्रसारित कीजिए -
(7x + 5)2
सर्वसमिका a2 + 2ab + b2 = (a + b)2 का प्रयोग करते हुए, निम्न के गुणनखंड कीजिए -
x2 + 14x + 49
4x2 + 4x + 1
सर्वसमिका a2 + 2ab + b2 = (a + b)2 का प्रयोग करते हुए, निम्न के गुणनखंड कीजिए -
सर्वसमिका a2 + 2ab + b2 = (a + b)2 का प्रयोग करते हुए, निम्न के गुणनखंड कीजिए -
16x2 + 40x + 25
सर्वसमिका a2 + 2ab + b2 = (a + b)2 का प्रयोग करते हुए, निम्न के गुणनखंड कीजिए -
`x^2/4 + 2x + 4`
यदि p + q = 12 और pq = 22 है, तो p2 + q2 ज्ञात कीजिए।
यदि a + b = 25 और a2 + b2 = 225 है, तो ab ज्ञात कीजिए।
नीचे दिए चित्र में कार्डों को उपयुक्त संख्या में लीजिए जिनमें [G(x × x)] जो x2 निरूपित करता है, R(x × 1) जो x निरूपित करता है तथा Y(1 × 1) जो 1] निरूपित करता है। इन कार्डों को आयतों के रूप में व्यवस्थित करके निम्न व्यंजकों के गुणनखंड कीजिए -
- 2x2 + 6x + 4
- x2 + 4x + 4
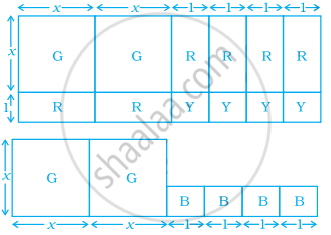
उपरोक्त आकृति का क्षेत्रफल परिकलित कौजिए।
