Advertisements
Advertisements
Question
निम्नलिखित आकृति में, BA || ED और BC || EF है। दर्शाइए कि ∠ABC + ∠DEF = 180° है।
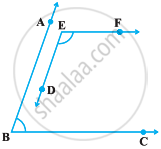
Solution
यह हमें दिया गया है -
BA || ED
BC || EF
यह दर्शाने के लिए - ∠ABC + ∠DEF = 180°
आइए DE को बढ़ाकर BC को G पर प्रतिच्छेद करें और EF को BA पर H पर प्रतिच्छेद करें।
तब, आकृति बन जाती है।
चूंकि, BA || DE
⇒ BA || GE
हमारे पास दो समानांतर रेखाएँ BA और GE हैं और BG एक तिर्यक रेखा है जो BA और GE को क्रमशः बिंदु B और G पर प्रतिच्छेद करती है।
⇒ ∠ABC = ∠EGC ...(i)
इसके अलावा, BC || EF और GE एक तिर्यक रेखा है जो BC और EF को क्रमश: G और E पर प्रतिच्छेद करती है।
⇒ ∠EGC = ∠HEG ...(ii)
चूँकि GE रेखा HF पर खड़ी एक किरण है।
रैखिक युग्म अभिगृहीत द्वारा,
∠HEG + ∠GEF = 180°
⇒ ∠EGC + ∠GEF = 180° ...[समीकरण (ii) से]
⇒ ∠ABC + ∠GEF = 180°
⇒ ∠ABC + ∠DEF = 180°
अत:, सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
आकृति में, x और y के मान ज्ञात कीजिए और फिर दर्शाइए कि AB || CD है।

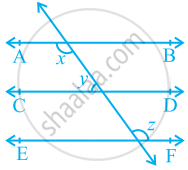
आकृति में, यदि AB || CD, CD || EF और y : z = 3 : 7 है, तो x का मान ज्ञात कीजिए।
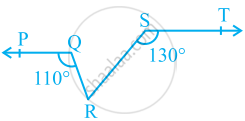
आकृति में, यदि PQ || ST, ∠PQR = 110° और ∠RST = 130° है, तो ∠QRS ज्ञात कीजिए।
[संकेत: बिंदु R से होकर ST के समांतर एक रेखा खिंचिए।]
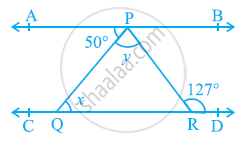
आकृति में, यदि AB || CD, ∠APQ = 50° और ∠PRD = 127° है, तो x और Y ज्ञात कीजिए।
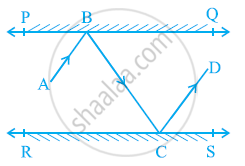
आकृति में, PQ और RS दो दर्पण है जो एक दूसरे के समांतर रखे गए है। एक आपतन किरण (incident ray) AB, दर्पण PQ से B पर टकराती है और परावर्तित किरण (reflected ray) पथ BC पर चलकर दर्पण RS से C पर टकराती है तथा पुनः CD के अनुदिश परावर्तित हो जाती है। सिद्ध कीजिए कि AB || CD है।
निम्नलिखित आकृति में, BA || ED और BC || EF है। दर्शाइए कि ∠ABC = ∠DEF है।
[संकेत : DE को आगे बढ़ाइए ताकि वह BC को, मान लीजिए P पर प्रतिच्छेद करें।]
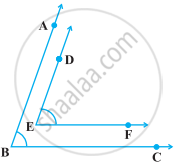
निम्नलिखित आकृति में, DE || QR तथा AP और BP क्रमश: कोणों ∠EAB और ∠RBA के समद्विभाजक हैं। ∠APB ज्ञात कीजिए।
किसी त्रिभुज के कोणों का अनुपात 2 : 3 : 4 है। इस त्रिभुज के तीनों कोण ज्ञात कीजिए।
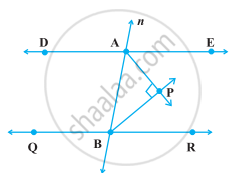
एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करती है। सिद्ध कीजिए कि इस प्रकार बने संगत कोणों के युग्म के समद्विभाजक समांतर होते हैं।
सिद्ध कीजिए कि दो रेखाएँ जो क्रमशः दो प्रतिच्छेदी रेखाओं पर लम्ब हो, परस्पर प्रतिच्छेद करती है।
[संकेत : विरोधाभास द्वारा उपपत्ति का प्रयोग कीजिए।
