Advertisements
Advertisements
Question
आकृति में, PQ और RS दो दर्पण है जो एक दूसरे के समांतर रखे गए है। एक आपतन किरण (incident ray) AB, दर्पण PQ से B पर टकराती है और परावर्तित किरण (reflected ray) पथ BC पर चलकर दर्पण RS से C पर टकराती है तथा पुनः CD के अनुदिश परावर्तित हो जाती है। सिद्ध कीजिए कि AB || CD है।
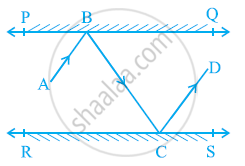
Solution
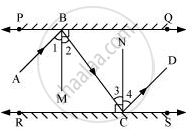
दिया है: PQ || RS और AB एक आपतन कोण है, CD एक परावर्तित किरण है।
सिद्ध करना है: AB || CD
रचना: BM ⊥ PQ और CN ⊥ RS खिंचा।
प्रमाण: BM ⊥ PQ और CN ⊥ RS
∴ BM || CM और BC एक तिर्यक रेखा है।
∴ ∠2 = ∠3 ...(1) ...(एकांतर अंत: कोण)
जबकि हम जानते है कि -
आपतन कोण = परावर्तित कोण, जहाँ BM और CN लंब हैं।
∴ ∠1 = ∠2 ...(2)
इसीप्रकार,
∴ ∠3 = ∠4 ...(3)
समीकरण (1) (2) और (3) से हम पाते है।
∠1 = ∠4 ...(4)
समीकरण (1) तथा (4) को जोड़ने पर
∠1 + ∠2 = ∠3 + ∠4
∠ABC = ∠BCD ...(एकांतर अत: कोण)
इसलिए, AB || CD
APPEARS IN
RELATED QUESTIONS
आकृति में, x और y के मान ज्ञात कीजिए और फिर दर्शाइए कि AB || CD है।

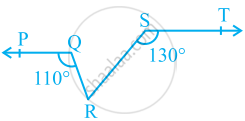
आकृति में, यदि AB || CD, EF ⊥ CD और ∠GED = 126° है, तो ∠AGE, ∠GEF और ∠FGE ज्ञात कीजिए।
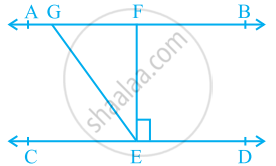
आकृति में, यदि PQ || ST, ∠PQR = 110° और ∠RST = 130° है, तो ∠QRS ज्ञात कीजिए।
[संकेत: बिंदु R से होकर ST के समांतर एक रेखा खिंचिए।]
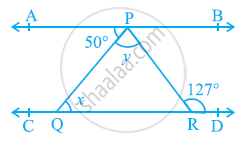
आकृति में, यदि AB || CD, ∠APQ = 50° और ∠PRD = 127° है, तो x और Y ज्ञात कीजिए।
दो रेखाएँ l और m एक ही रेखा n पर लंब हैं। क्या l और m परस्पर लंब हैं? अपने उत्तर के लिए कारण दीजिए।
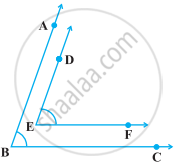
निम्नलिखित आकृति में, BA || ED और BC || EF है। दर्शाइए कि ∠ABC = ∠DEF है।
[संकेत : DE को आगे बढ़ाइए ताकि वह BC को, मान लीजिए P पर प्रतिच्छेद करें।]
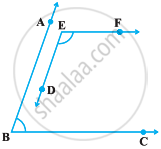
निम्नलिखित आकृति में, BA || ED और BC || EF है। दर्शाइए कि ∠ABC + ∠DEF = 180° है।
किसी त्रिभुज के कोणों का अनुपात 2 : 3 : 4 है। इस त्रिभुज के तीनों कोण ज्ञात कीजिए।
एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करती है। सिद्ध कीजिए कि इस प्रकार बने संगत कोणों के युग्म के समद्विभाजक समांतर होते हैं।
सिद्ध कीजिए कि दो रेखाएँ जो क्रमशः दो प्रतिच्छेदी रेखाओं पर लम्ब हो, परस्पर प्रतिच्छेद करती है।
[संकेत : विरोधाभास द्वारा उपपत्ति का प्रयोग कीजिए।
