Question

निम्नलिखित के लिए धातु के क्रिस्टल में संकुलन क्षमता की गणना कीजिए।

अन्त:केन्द्रित घनीय

(यह मानते हुए कि परमाणु एक-दूसरे के सम्पर्क में हैं।)

Answer 1

संलग्न चित्र से यह स्पष्ट है कि केन्द्र पर स्थित परमाणु विकर्ण पर व्यवस्थित अन्य दो परमाणुओं के सम्पर्क में है।

Δ EFD में,

b² = a² + a² = 2a²

b = `sqrt2`a

अब Δ AFD में,

c² = a² + b² = a² + 2a² = 3a²

c = `sqrt3`a

काय विकर्ण 4r की लम्बाई 47 के बराबर है, जहाँ r गोले (परमाणु) का अर्द्धव्यास है क्योंकि विकर्ण पर उपस्थित तीनों गोले एक-दूसरे के सम्पर्क में हैं। अतः

`sqrt3`a = 4r

a = `"4r"/sqrt3`

अतः यह भी लिख सकते हैं कि r = `sqrt3/4`a

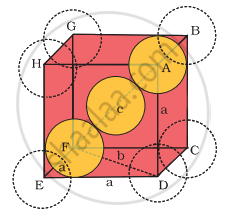
अंत्य केंद्रित घनीय एकक कोष्टिका (के विकर्ण पर उपस्थित गोलों को ठोस परिसीमा द्वारा दर्शाया गया है।)

इस प्रकार की संरचना में परमाणुओं की कुल संख्या 2 है तथा उनका आयतन 2 x (4/3) πr³ है।

घन का आयतन a³, `(4/sqrt3 "r")^3` के बराबर होगा अथवा `"a"^3 = (4/sqrt3 "r")^3` अत:

संकुलन क्षमता = `("एकक कोष्टिका में दो गोलों द्वारा अध्यासित आयतन" xx 100)/("एकक कोष्टिका का कुल आयतन")`

`= (2 xx (4//3) pi"r"^3 xx 100)/(4//sqrt3"r")^3`%

`= ((8//3)pi"r"^3 xx 100)/(64//(3sqrt3)"r"^3)`%

= 68%