Advertisements
Advertisements
Question
On dividing x3 – 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and –2x + 4, respectively. Find g(x)
Solution
p(x) = x3-3x2+x+2 (Dividend)
g(x) = ? (Divisor)
Quotient = (x - 2)
Remainder = (-2x + 4)
Dividend = Divisor × Quotient + Remainder
x3 - 3x2 + x + 2 = g(x) x (x - 2) + (-2x + 4)
x3 - 3x2 + x + 2 +2x - 4 = g(x)(x - 2)
x3 - 3x2 + 3x - 2 = g(x)(x - 2)
g(x) is the quotient when we divide (x3 -3x2 + 3x - 2) by (x - 2)
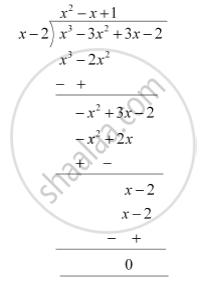
∴ g(x) = (x^2 - x + 1)
APPEARS IN
RELATED QUESTIONS
Apply division algorithm to find the quotient q(x) and remainder r(x) on dividing f(x) by g(x) in the following f(x) = 10x4 + 17x3 − 62x2 + 30x − 3, g(x) = 2x2 + 7x + 1
Apply division algorithm to find the quotient q(x) and remainder r(x) on dividing f(x) by g(x) in the following f(x) = 4x3 + 8x2 + 8x + 7, g(x) = 2x2 − x + 1
What must be added to the polynomial f(x) = x4 + 2x3 − 2x2 + x − 1 so that the resulting polynomial is exactly divisible by x2 + 2x − 3 ?
Find all the zeros of the polynomial x3 + 3x2 − 2x − 6, if two of its zeros are `-sqrt2` and `sqrt2`
Verify division algorithm for the polynomial `f(x)= (8 + 20x + x^2 – 6x^3) by g(x) =( 2 + 5x –3x^2).`
Find the quotient and remainder of the following.
(8x3 – 1) ÷ (2x – 1)
The base of a parallelogram is (5x + 4). Find its height if the area is 25x2 – 16
Can x2 – 1 be the quotient on division of x6 + 2x3 + x – 1 by a polynomial in x of degree 5?
If on division of a polynomial p(x) by a polynomial g(x), the quotient is zero, what is the relation between the degrees of p(x) and g(x)?
For which values of a and b, are the zeroes of q(x) = x3 + 2x2 + a also the zeroes of the polynomial p(x) = x5 – x4 – 4x3 + 3x2 + 3x + b? Which zeroes of p(x) are not the zeroes of q(x)?
