Advertisements
Advertisements
Question
On increasing the radii of the base and the height of a cone by 20%, its volume will increase by
Options
20%
40%
60%
72.8%
Solution
72.8%
Let the original radius of the cone be r and height be h.
Then, original volume`=1/3 pi"r"^2"h"`
`"Let" 1/3 pir^2"h" = V`
New radius = 120% of r
`=120/100`
`= (6r)/5`
New height = 120% of h
`=(120"h")/100`
`= (6"h")/ 5`
Hence, the new volume `= 1/3 pi xx((6"r")/5)^2xx"6h"/5`
`=216/125(1/3pi"r"^2"h")`
`=216/125 "V"`
Increase in Volume `= ((216)/(125)"v"-"V")`
`=(91"V")/(125)`
Increase in % of the volume `= ((991"V"))/125 xx 1/Vxx100)%`
`= 72.8 %`
APPEARS IN
RELATED QUESTIONS
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboids are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see the following figure). Use [π = `22/7`]

50 circular plates each of diameter 14cm and thickness 0.5cm are placed one above other to form a right circular cylinder. Find its total surface area?
25 circular plates each of radius 10.5cm and thickness 1.6cm are placed one above the other to form a solid circular cylinder. Find the curved surface area and volume of cylinder so formed?
How many coins 1.75cm in diameter and 2mm thick must be melted to form a cuboid 11cm x 10cm x 75cm___?
A solid consists of a circular cylinder surmounted by a right circular cone. The height of the cone is h. If the total height of the solid is 3 times the volume of the cone, then the height of the cylinder is
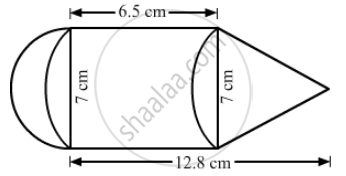
The adjoining figure represents a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other. Find the volume of the solid.
A cubical ice-cream brick of edge 22 cm is to be distributed among some children by filling ice-cream cones of radius 2 cm and height 7 cm up to the brim. How many children will get the ice-cream cones?
The volumes of two cubes are in the ratio 1 : 27. The ratio of their surface area is
The radius of a solid right circular cylinder decreases by 20% and its height increases by 10%. Find the percentage change in its : curved surface area.
A rectangular water tank of base 11 m × 6 m contains water upto a height of 5 m. If the water in the tank is transferred to a cylindrical tank of radius 3.5 m, find the height of the water level in the tank.
