Advertisements
Advertisements
Question
P is the centre of the circle and its radius is
10 cm. Distance of a chord AB from the centre is 6 cm. Find the length of chord AB.
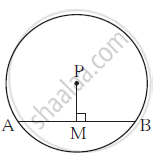
Solution
seg PM ⊥ chord AB
In right angled triangle Δ APM
AM2 + PM2 = AP2 ........ (by Pythagoras theorem)
∴ AM2 + 62 = 102
∴ AM2 = 100 - 36
∴ AM2 = 64
∴ AM = 8 cm 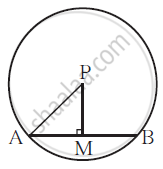
We know perpendicular from centre bisects the chord so AM = MB
∴ AB = 2 × AM
∴ AB = 2 × 8
∴ AB = 16 cm
∴ lenght of chord AB = 16 cm.
APPEARS IN
RELATED QUESTIONS
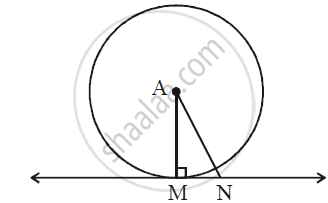
In the following figure, point ‘A’ is the centre of the circle. Line MN is tangent at point M. If AN = 10 cm and MN = 5 cm, determine radius of the circle.
Height of a cylindrical barrel is 50 cm and radius of its base is 20 cm. Anurag started to fill the barrel with water, when it was empty, by a cylindrical mug. The diameter and height of the mug was 10 cm and 15cm respectively. How many minium number of mugs will be required for the barrel to overflow?
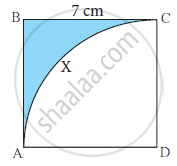
Side of square ABCD is 7 cm. With D as the centre and DA as radius, arc AXC is drawn.Find the area of the shaded region with the help of the following flow chart .

There is a hemispherical bowl. A cone is to be made such that, if it is filled with water twice and the water is poured in the bowl, it will be filled just completely. State how will you decide the radius and perpendicular height of the cone.
In the figure, line l touches the circle with center O at point P. Q is the midpoint of radius OP. RS is a chord through Q such that chords RS || line l. If RS = 12, find the radius of the circle.

In the given figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent, which touches the circle at point T. seg AP ⊥ line PQ and seg BQ ⊥ line PQ. Prove that, seg CP ≅ seg CQ.

Draw the tangent at any point M on the circle with centre O and radius 2.9 cm.
Draw a tangent at any point ‘M’ on the circle of radius 3.3 cm and centre ‘O’.
In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. What is the measure of ∠CAB? Why?

In the adjoining figure, the line MN touches the circle with center A at point M. If AN = 13 and MN = 5, then find the radius of the circle?

AP is a tangent at A drawn to the circle with centre O from an external point P. OP = 12 cm and ∠OPA = 30°, then the radius of a circle is ______.
