Advertisements
Advertisements
Question
‘P’ केंद्र वाले वृत्त की त्रिज्या 10 सेमी है। जीवा AB द्वारा वृत्त केंद्र पर समकोण बनाया गया हो, तो द्वैत्रिज्य का क्षेत्रफल ज्ञात करने के लिए निम्न कृति पूर्ण कीजिए। (π = 3.14)
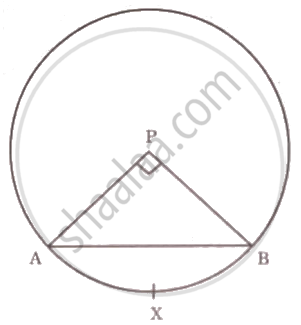
कृति:
r = 10 सेमी, θ = 90°, π = 3.14
A(P − AXB) = `θ/360 xx square`
= `square/360 xx 3.14 xx 10^2`
= `1/4 xx square`
A (P − AXB) = `square` वर्ग सेमी
Activity
Sum
Solution
r = 10 सेमी, θ = 90°, π = 3.14
A(P − AXB) = \[\frac\theta{360}\] × \[\boxed{\pi r^2}\]
= \[\frac{\boxed{90}}{360}\] × 3.14 × 102
= \[\frac{1}{4}\] × \[\boxed{3.14}\] × \[\boxed{100}\]
A(P − AXB) = \[\boxed{78.5}\] वर्ग सेमी
shaalaa.com
Is there an error in this question or solution?
