Advertisements
Advertisements
Question
Point (–3, 5) lies in the ______.
Options
first quadrant
second quadrant
third quadrant
fourth quadrant
Solution
Point (–3, 5) lies in the second quadrant.
Explanation:
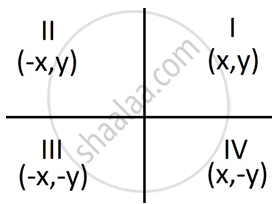
(–3, 5) is of the form (–x, y).
APPEARS IN
RELATED QUESTIONS
Let ABCD be a square of side 2a. Find the coordinates of the vertices of this square when The centre of the square is at the origin and coordinate axes are parallel to the sides AB and AD respectively.
Find the points of trisection of the line segment joining the points:
5, −6 and (−7, 5),
Find the points of trisection of the line segment joining the points:
(3, -2) and (-3, -4)
The points (3, -4) and (-6, 2) are the extremities of a diagonal of a parallelogram. If the third vertex is (-1, -3). Find the coordinates of the fourth vertex.
If the point C ( - 2,3) is equidistant form the points A (3, -1) and Bx (x ,8) , find the value of x. Also, find the distance between BC
Find the ratio in which the point (-1, y) lying on the line segment joining points A(-3, 10) and (6, -8) divides it. Also, find the value of y.
What is the distance between the points (5 sin 60°, 0) and (0, 5 sin 30°)?
If the distance between points (x, 0) and (0, 3) is 5, what are the values of x?
If the centroid of the triangle formed by the points (3, −5), (−7, 4), (10, −k) is at the point (k −1), then k =
If the points P(1, 2), Q(0, 0) and R(x, y) are collinear, then find the relation between x and y.
Given points are P(1, 2), Q(0, 0) and R(x, y).
The given points are collinear, so the area of the triangle formed by them is `square`.
∴ `1/2 |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)| = square`
`1/2 |1(square) + 0(square) + x(square)| = square`
`square + square + square` = 0
`square + square` = 0
`square = square`
Hence, the relation between x and y is `square`.
