Advertisements
Advertisements
Question
Prove that, any rectangle is a cyclic quadrilateral
Solution
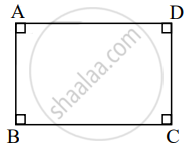
Given: ▢ABCD is a rectangle.
To prove: ▢ABCD is a cyclic quadrilateral
Proof:
▢ABCD is a rectangle. ....[Given]
∴ ∠A = ∠B = ∠C = ∠D = 90° ....[Angles of a rectangle]
Now, ∠A + ∠C = 90° + 90°
∴ ∠A + ∠C = 180°
We know, if a pair of opposite angles of a quadrilateral is supplementary, then the quadrilateral is cyclic.
∴ ▢ABCD is a cyclic quadrilateral ......[Converse of cyclic quadrilateral theorem]
So, any rectangle is a cyclic quadrilateral.
RELATED QUESTIONS
Prove that the “the opposite angles of the cyclic quadrilateral are supplementary”.
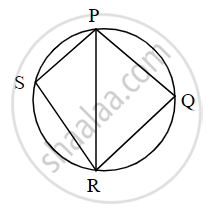
In the given figure, ▢PQRS is cyclic. side PQ ≅ side RQ. ∠PSR = 110°, Find -
(1) measure of ∠PQR
(2) m(arc PQR)
(3) m(arc QR)
(4) measure of ∠PRQ
`square`MRPN is cyclic, ∠R = (5x – 13)°, ∠N = (4x + 4)°. Find measures of ∠R and ∠N.
In the given figure, line PR touches the circle at point Q. Answer the following questions with the help of the figure.
(1) What is the sum of ∠ TAQ and ∠ TSQ ?
(2) Find the angles which are congruent to ∠ AQP.
(3) Which angles are congruent to ∠ QTS ?
(4) ∠TAS = 65°, find the measure of ∠TQS and arc TS.
(5) If ∠AQP = 42°and ∠SQR = 58° find measure of ∠ATS.

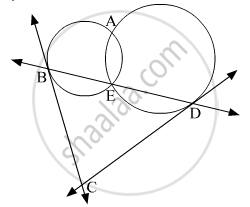
In the given figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that ▢ABCD is cyclic.
Find the value of x in the given figure.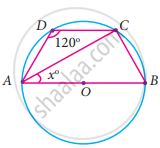
A school wants to conduct tree plantation programme. For this a teacher allotted a circle of radius 6 m ground to nineth standard students for planting sapplings. Four students plant trees at the points A, B, C and D as shown in figure. Here AB = 8 m, CD = 10 m and AB ⊥ CD. If another student places a flower pot at the point P, the intersection of AB and CD, then find the distance from the centre to P.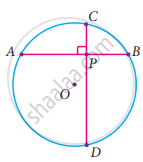
MRPN is cyclic, ∠R = (5x – 13)°, ∠N = (4x + 4)°. Find measures of ∠R and ∠N, by completing the following activity.
Solution:
MRPN is cyclic
The opposite angles of a cyclic square are `square`
∠R + ∠N = `square`
∴ (5x – 13)° + (4x + 4)° = `square`
∴ 9x = 189°
∴ x = `square`
∴ ∠R = (5x – 13)° = `square`
∴ ∠N = (4x + 4)° = `square`
Prove the following theorems:
Opposite angles of a cyclic quadrilateral are supplementary.
In the figure, PQRS is cyclic, side PQ ≅ side RQ, ∠PSR = 110°. Find

(i) measure of ∠PQR
(ii) m(arc PQR)
(iii) m(arc QR)
If two consecutive angles of cyclic quadrilateral are congruent, then prove that one pair of opposite sides is congruent and other is parallel.
