Question

Prove that for an astroid  `   x^(2/3) +y2/3= a^(2/3)` the line 𝜽=𝝅/𝟔 Divide the arc in the first quadrant in a ratio 1:3. 

 

Answer 1

Given curve : astroid` x^(2/3)+y^(2/3) = a^(2/3)`

The line 𝜽=𝝅/𝟔 cuts the asroid in 1 st quadrant. 

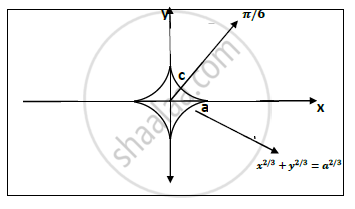
C is the point on the curve which cuts the arc.
Length of astroid in first quadrant: 

Put `  x = acos^3t and y=asin^3t` 

`dx=-3 asin t.cos^2tdt    dy=3 acos t.sin^2tdt`

`s= int_0^(pi/2) sqrt ((dx/dt)^2+(dy/dt)^2)=int_0^(pi/2) sqrt((-3asin t.cos^2 t)^2+(3 acos t .sin^2 t )^2)` dt 

= `int_0^(pi/2) 3a.sin t.cost dt` 

= `3/2 a  int_0^(pi/2) sin 2t  dt` 

=`3/4 a [-cos 2t ]_0^(pi/2) `

∴ `s= 3/2 a `                        ………………….(1) 

Now the length of the curve ac : Just put `pi/6` 𝒊𝒏𝒔𝒕𝒆𝒅 𝒐𝒇 `pi/2`  because the curve is Only upto given line. 

∴ S(ac) =`int_0^(pi/6) 3a sint . cost dt =3/4a [-cos 2t]_0^(pi/6) ` 

=` 3/4 a [-1/2+1]` 

`s(ac)= 3/8 a  `                              ……………(2) 

Legnth of remaining part = `3/2a-3/8 a=9/8 a`  ……………….(3)

Divide eqn (3) and (2).
The line `pi/6` cuts the given astroid in the ratio of 1:3
Hence proved.