Advertisements
Advertisements
Question
Prove that, if a diameter of a circle bisects two chords of the circle then those two chords are parallel to each other.
Solution
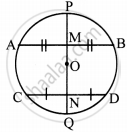
Given:
- O is the centre of the circle.
- seg PQ is the diameter.
- Diameter PQ bisects the chords AB and CD at the points M and N respectively.
To prove: chord AB || chord CD.
Proof:
Point M is the midpoint of chord AB. ...(Given)
∴ seg OM ⊥ chord AB ...(The line segment joining the center of the circle and the midpoint of the chord is perpendicular to the chord.)
∴ ∠OMA = 90° ...(i)
Point N is the midpoint of chord CD. ...(Given)
∴ seg ON ⊥ chord CD ...(The line segment joining the center of the circle and the midpoint of the chord is perpendicular to the chord.)
∴ ∠ONC = 90° ...(ii)
Now, ∠OMA + ∠ONC
= 90° + 90° ...[From (i) and (ii)]
∴ ∠OMA + ∠ONC = 180°
But, ∠OMA and ∠ONC form a pair of interior angles on lines AB and CD when ∠MN is their transversal.
∴ chord AB || chord CD ...(Interior angles test)
APPEARS IN
RELATED QUESTIONS
Distance of chord AB from the centre of a circle is 8 cm. Length of the chord AB is 12 cm. Find the diameter of the circle.
Diameter of a circle is 26 cm and length of a chord of the circle is 24 cm. Find the distance of the chord from the centre.
Radius of a circle is 34 cm and the distance of the chord from the centre is 30 cm, find the length of the chord.
Radius of a circle with centre O is 41 units. Length of a chord PQ is 80 units, find the distance of the chord from the centre of the circle.
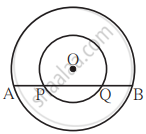
In the given figure, centre of two circles is O. Chord AB of bigger circle intersects the smaller circle in points P and Q. Show that AP = BQ.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is ______.
The length of the longest chord of the circle with radius 2.9 cm is ______.
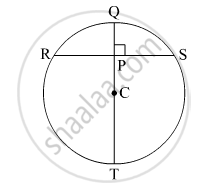
In the given figure, C is the centre of the circle. seg QT is a diameter CT = 13, CP = 5, find the length of chord RS.
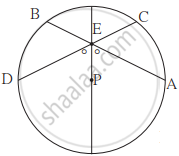
In the given figure, P is the centre of the circle. chord AB and chord CD intersect on the diameter at the point E. If ∠AEP ≅ ∠DEP then prove that AB = CD.
In the given figure, CD is a diameter of the circle with centre O. Diameter CD is perpendicular to chord AB at point E. Show that ΔABC is an isosceles triangle.

