Advertisements
Advertisements
Question
Prove that the points (0 , -4) , (6 , 2) , (3 , 5) and (-3 , -1) are the vertices of a rectangle.
Solution
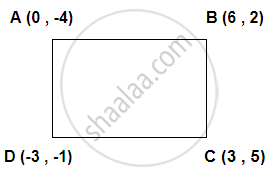
AB = `sqrt ((6 - 0)^2 + (2 + 4)^2) = 6 sqrt 2` units
BC = `sqrt ((6 - 3)^2 + (2 - 5)^2) = 3 sqrt 2` units
CD = `sqrt ((3 + 3)^2 + (5 + 1)^2) = 6 sqrt 2` units
DA = `sqrt ((- 3 - 0)^2 + (-1 + 4)^2) = 3 sqrt 2` units
AC = `sqrt ((3 - 0)^2 + (5 + 4)^2) = 3 sqrt 10` units
BD = `sqrt ((6 + 3)^2 + (2 + 1)^2) = 3 sqrt 10` units
∵ AB = CD and BC = DA ,
Also AC = BD
∴ ABCD is a rectangle.
APPEARS IN
RELATED QUESTIONS
If A(4, 3), B(-1, y) and C(3, 4) are the vertices of a right triangle ABC, right-angled at A, then find the value of y.
If P and Q are two points whose coordinates are (at2 ,2at) and (a/t2 , 2a/t) respectively and S is the point (a, 0). Show that `\frac{1}{SP}+\frac{1}{SQ}` is independent of t.
The value of 'a' for which of the following points A(a, 3), B (2, 1) and C(5, a) a collinear. Hence find the equation of the line.
Prove that the points (1 , 1) , (-1 , -1) and (`- sqrt 3 , sqrt 3`) are the vertices of an equilateral triangle.
Find the distance between the points (a, b) and (−a, −b).
Find the distance between the following pairs of points:
`(3/5,2) and (-(1)/(5),1(2)/(5))`
Given A = (3, 1) and B = (0, y - 1). Find y if AB = 5.
Show that the points (0, –1), (8, 3), (6, 7) and (– 2, 3) are vertices of a rectangle.
Seg OA is the radius of a circle with centre O. The coordinates of point A is (0, 2) then decide whether the point B(1, 2) is on the circle?
A circle drawn with origin as the centre passes through `(13/2, 0)`. The point which does not lie in the interior of the circle is ______.
