Advertisements
Advertisements
प्रश्न
Prove that the points (0 , -4) , (6 , 2) , (3 , 5) and (-3 , -1) are the vertices of a rectangle.
उत्तर
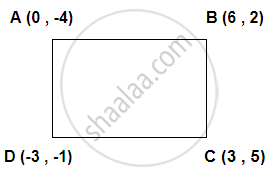
AB = `sqrt ((6 - 0)^2 + (2 + 4)^2) = 6 sqrt 2` units
BC = `sqrt ((6 - 3)^2 + (2 - 5)^2) = 3 sqrt 2` units
CD = `sqrt ((3 + 3)^2 + (5 + 1)^2) = 6 sqrt 2` units
DA = `sqrt ((- 3 - 0)^2 + (-1 + 4)^2) = 3 sqrt 2` units
AC = `sqrt ((3 - 0)^2 + (5 + 4)^2) = 3 sqrt 10` units
BD = `sqrt ((6 + 3)^2 + (2 + 1)^2) = 3 sqrt 10` units
∵ AB = CD and BC = DA ,
Also AC = BD
∴ ABCD is a rectangle.
APPEARS IN
संबंधित प्रश्न
Find the distance between the points
P(a + b,a - b)andQ(a -b,a + b)
Find the distance between the following pair of points.
L(5, –8), M(–7, –3)
Find the distance between the following point :
(Sin θ - cosec θ , cos θ - cot θ) and (cos θ - cosec θ , -sin θ - cot θ)
P and Q are two points lying on the x - axis and the y-axis respectively . Find the coordinates of P and Q if the difference between the abscissa of P and the ordinates of Q is 1 and PQ is 5 units.
Prove that the points (0 , 0) , (3 , 2) , (7 , 7) and (4 , 5) are the vertices of a parallelogram.
Show that the points (2, 0), (–2, 0), and (0, 2) are the vertices of a triangle. Also, a state with the reason for the type of triangle.
Prove that the points A (1, -3), B (-3, 0) and C (4, 1) are the vertices of an isosceles right-angled triangle. Find the area of the triangle.
If the point (x, y) is at equidistant from the point (a + b, b – a) and (a-b, a + b). Prove that ay = bx.
AOBC is a rectangle whose three vertices are A(0, 3), O(0, 0) and B(5, 0). The length of its diagonal is ______.
The points A(–1, –2), B(4, 3), C(2, 5) and D(–3, 0) in that order form a rectangle.
