Advertisements
Advertisements
प्रश्न
Prove that the points A (1, -3), B (-3, 0) and C (4, 1) are the vertices of an isosceles right-angled triangle. Find the area of the triangle.
उत्तर
AB =`sqrt((-3 -1)^2 + (0 +3)^2) = sqrt(16+9) = sqrt(25)` = 5
BC =`sqrt((4 + 3)^2 + (1 +0)^2)= sqrt(49+1)= sqrt(50) = 5sqrt(2)`
CA =`sqrt((1 -4)^2 + (-3 - 1)^2) = sqrt(9 + 16) = sqrt(25)` = 5
∵ AB = CA
A, B, C are the vertices of an isosceless triangle.
AB2 + CA2 = 25 + 25 = 50
BC2 = `(5sqrt(2))^2` = 50
∴ AB2 + CA2 = BC2
Hence, A, B, C are the vertices of a right-angled triangle.
Hence, ΔABC is an isosceles right-angled triangle.
Area of ΔABC = `(1)/(2) xx "AB" xx "CA"`
= `(1)/(2) xx 5 xx 5`
= 12.5 sq.units
APPEARS IN
संबंधित प्रश्न
If A(4, 3), B(-1, y) and C(3, 4) are the vertices of a right triangle ABC, right-angled at A, then find the value of y.
Show that four points (0, – 1), (6, 7), (–2, 3) and (8, 3) are the vertices of a rectangle. Also, find its area
If the distance between the points (4, k) and (1, 0) is 5, then what can be the possible values of k?
Find the distance between the points
A(-6,-4) and B(9,-12)
Using the distance formula, show that the given points are collinear:
(6, 9), (0, 1) and (-6, -7)
Determine whether the points are collinear.
L(–2, 3), M(1, –3), N(5, 4)
If A and B are the points (−6, 7) and (−1, −5) respectively, then the distance
2AB is equal to
Find the relation between a and b if the point P(a ,b) is equidistant from A (6,-1) and B (5 , 8).
P and Q are two points lying on the x - axis and the y-axis respectively . Find the coordinates of P and Q if the difference between the abscissa of P and the ordinates of Q is 1 and PQ is 5 units.
Prove that the points (0,3) , (4,3) and `(2, 3+2sqrt 3)` are the vertices of an equilateral triangle.
Prove that the points (5 , 3) , (1 , 2), (2 , -2) and (6 ,-1) are the vertices of a square.
From the given number line, find d(A, B):

A point P lies on the x-axis and another point Q lies on the y-axis.
If the abscissa of point P is -12 and the ordinate of point Q is -16; calculate the length of line segment PQ.
Points A (-3, -2), B (-6, a), C (-3, -4) and D (0, -1) are the vertices of quadrilateral ABCD; find a if 'a' is negative and AB = CD.
The point which divides the lines segment joining the points (7, -6) and (3, 4) in ratio 1 : 2 internally lies in the ______.
The point which lies on the perpendicular bisector of the line segment joining the points A(–2, –5) and B(2, 5) is ______.
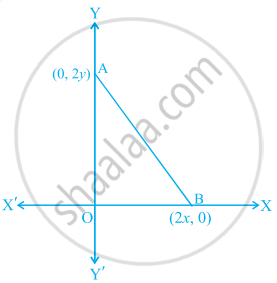
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is ______.
Find a point which is equidistant from the points A(–5, 4) and B(–1, 6)? How many such points are there?
If the point A(2, – 4) is equidistant from P(3, 8) and Q(–10, y), find the values of y. Also find distance PQ.
If (a, b) is the mid-point of the line segment joining the points A(10, –6) and B(k, 4) and a – 2b = 18, find the value of k and the distance AB.
