Advertisements
Advertisements
प्रश्न
A point P lies on the x-axis and another point Q lies on the y-axis.
If the abscissa of point P is -12 and the ordinate of point Q is -16; calculate the length of line segment PQ.
उत्तर
The co-ordinates of P and Q are (-12, 0) and (0, -16) respectively.
PQ = `sqrt((-12 - 0)^2 + (0 + 16)^2)`
= `sqrt(144 + 256)`
= `sqrt(400)`
= 20
APPEARS IN
संबंधित प्रश्न
Find the distance between the points
A(-6,-4) and B(9,-12)
If P (x , y ) is equidistant from the points A (7,1) and B (3,5) find the relation between x and y
Find the distance between the following pair of point.
T(–3, 6), R(9, –10)
Find the distance between the following pairs of point.
W `((- 7)/2 , 4)`, X (11, 4)
Find the relation between x and y if the point M (x,y) is equidistant from R (0,9) and T (14 , 11).
x (1,2),Y (3, -4) and z (5,-6) are the vertices of a triangle . Find the circumcentre and the circumradius of the triangle.
Find the distance between the origin and the point:
(-5, -12)
Find the distance between the origin and the point:
(8, -15)
Prove that the points A (1, -3), B (-3, 0) and C (4, 1) are the vertices of an isosceles right-angled triangle. Find the area of the triangle.
KM is a straight line of 13 units If K has the coordinate (2, 5) and M has the coordinates (x, – 7) find the possible value of x.
By using the distance formula prove that each of the following sets of points are the vertices of a right angled triangle.
(i) (6, 2), (3, -1) and (- 2, 4)
(ii) (-2, 2), (8, -2) and (-4, -3).
If the point (x, y) is at equidistant from the point (a + b, b – a) and (a-b, a + b). Prove that ay = bx.
Find distance between point A(– 3, 4) and origin O
Find distance between point Q(3, – 7) and point R(3, 3)
Solution: Suppose Q(x1, y1) and point R(x2, y2)
x1 = 3, y1 = – 7 and x2 = 3, y2 = 3
Using distance formula,
d(Q, R) = `sqrt(square)`
∴ d(Q, R) = `sqrt(square - 100)`
∴ d(Q, R) = `sqrt(square)`
∴ d(Q, R) = `square`
Show that the points (0, –1), (8, 3), (6, 7) and (– 2, 3) are vertices of a rectangle.
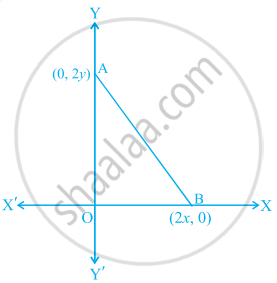
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is ______.
If (a, b) is the mid-point of the line segment joining the points A(10, –6) and B(k, 4) and a – 2b = 18, find the value of k and the distance AB.
The centre of a circle is (2a, a – 7). Find the values of a if the circle passes through the point (11, – 9) and has diameter `10sqrt(2)` units.
Show that Alia's house, Shagun's house and library for an isosceles right triangle.
